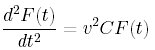第９章　それぞれの解　F(t)

さて、8章 では１つの方程式を2つに分けるために、ｘにもｔにも依存しない定数Ｃを持ち込むことにより無理やり二つに分ける、という
暴力的（？）手法をとってしまったので、今度はＣって何だ？という疑問が浮上してしまう。
9章、10章では、そのＣの数探しについてである。

まずは波動方程式の左辺だったF(t)について考えてみる。
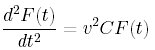これが元々の式。

１．C = 0 の場合

このとき、右辺は全滅してしまうので
となる。
もともとの式が2階微分の形なので、元の式に戻していこう。
1回積分して、1階微分の形にすると、
となる。仮に、出てくる定数をDと表す。
もう一度積分して、元の関数に戻すと
となる。
この式、数学的には解を持つ立派な方程式なのだが、直線の方程式であり、波の方程式ではない。
今求めたいのは弦（つまり波）の方程式なので、残念ながら適当ではない。

C = 0 は却下する。

２．C ≠ 0 の場合

この場合、0でなければ何でもいいかというと、そういうわけにもいかない。
もう一度
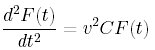の式に注目してほしい。
左辺にもF(t)が、右辺にもF(t)が登場している。このことが指し示しているのは
2階微分しても関数の形が変わらないものにしなければならないということ。

よって、候補となる関数は
　　　　　　 の4種類しかない。（α、βは実数とする）
1階微分
2階微分 となる。

2-1．C ＞ 0 の場合

先ほどの候補のうち、は係数が正になっている。（2階微分の前２つの式にはマイナスがついていない）
この場合、 と考えることができる。
もも別々に方程式を満たし、
の式は、とがどのような値でも方程式を満たす。
このような方程式を「任意定数（ , ）を含む一般解」という。

…が、指数関数は波にはならない。よって

C ＞ 0 は却下する。

2-2．C ＜ 0 の場合

先ほどの候補のうちは、係数が負になっている。（マイナスがついている）
この場合と考えることができる。
もも別々に方程式を満たし、
は、 と がどのような値でも方程式を満たす。（つまり一般解である）
…最も都合のいいことは、この式が三角関数でできているため波を表しているということである。

つまり C ＜ 0 ならよい。

ちなみに「本当に と にどんな値をいれても波になるの〜？」という疑問にお答えして（？）
この方程式で実際に計算している波のシュミレータを用意しましたので
適当な数を入れて遊んでみて下さいな。

さて、話はまだまだ続きます。

唐突に出てきたβであるが、これは何者だろうか？
について、考えてみる（別にcosでもかまわないのだが）
sinの周期は2πであるので、
となったときに1周期となる。つまり
が周期をあらわす。（周期って何だ！？という人は、後で 2章 を参照すること。） この式を変形すると
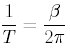これをβに関する式にすると
つまり、βは角周波数ωのことであることがわかった。
よって、書き直すと
となる。