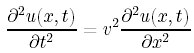第８章　変数分離

さて、前回までで一般の古典的波動方程式までたどりついたが、その式を少し変形しておく。
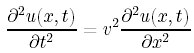これが、前回の方程式。この両辺をｖで割っておく。

この方程式は、残念ながらこのままでは解くことができない。
解けない方程式を解くにはどうしたらいいかというと、この方程式を解ける簡単な形に変換することができれば良い。
（別に解けなくてもいいじゃないか、という突っ込みはこの際無視する。）

つまり、どのような関数かわからないものを、とという別々の式を掛け合わせたものではないかと仮定したのである。
もも、それぞれは１つの関数に依存する数式なので解くことができる。
しかし、どのようにｘとｔがかかわっているか分からない関数を、単に掛け算として片付けてしまっていいのだろうか？

それを確かめるために
に代入してみよう。

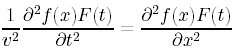微分に関係しないパラメータを外に出してしまおう

…これでは、まだ本当に大丈夫かどうかの判断がつかない。ので、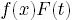で両辺を割ってみる。
（ちなみに1パラメータだけなので、普通微分dにもどします）

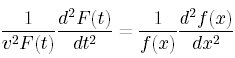
ここで、注目してほしいことは
左辺からはxが消えてｔのみの関数とすることができた。
右辺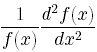からはtが消えてxのみの関数とすることができた。

問題は、左辺と右辺の等号が成り立たなくてはいけない。
それも、「ｘがどんな値でも」「yがどんな値でも」成り立たなくてはならない。

…そんなことはありえるのか？

ここで、ｘにもｔにも関係ない定数をCと定める。
左辺は

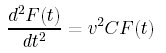
と変形することができる。
右辺は

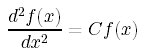
と変形することができる。

これで、１つの方程式から２つに変換することができた。

この一連の作業を「変数分離」という。