波動方程式の右辺であったf(x)についてである。
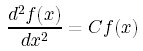 (元の式。)
(元の式。)
恐ろしく長い9章のわりに、この章はえらく短い。
波動方程式の右辺であったf(x)についてである。
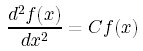 (元の式。)
(元の式。)
が、 9章と同様に
![]()
という式に変換することができる。
![]() は「ガンマ」と読む。英語ではgammaと書く。
は「ガンマ」と読む。英語ではgammaと書く。
この場合、![]() となるわけだが、さて
となるわけだが、さて![]() とは何者であろうか?
とは何者であろうか?
![]() について考えてみると、1周期が2πであるので
について考えてみると、1周期が2πであるので
![]() が1周期をあらわし、
が1周期をあらわし、
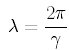 として、波長をあらわすことができる。(波長って!?という方は 2章をどうぞ)
として、波長をあらわすことができる。(波長って!?という方は 2章をどうぞ)
これまた 9章と同じように変形していくと
![]()
![]() つまり、
つまり、![]() は波数についてあらわしていたのだった。
は波数についてあらわしていたのだった。
さて、 9章で出てきた
![]() を考慮に入れると
を考慮に入れると
![]() のような式になる。
のような式になる。
βやγにそれぞれ代入すると
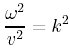 という形になる。これを速さについて解くと
という形になる。これを速さについて解くと
![]() という形になり、性質上マイナスはありえないので
という形になり、性質上マイナスはありえないので
![]() という形になる。つまり、速さは角周波数と波数によって導き出すことができる。
という形になる。つまり、速さは角周波数と波数によって導き出すことができる。