 dinger 方程式
dinger 方程式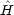
 = E
= E で, E0 を最低固有値,
で, E0 を最低固有値,  0 を対応する固有関数とするとき,任意の関数
0 を対応する固有関数とするとき,任意の関数  について次の関係が成立する。(変分原理)
について次の関係が成立する。(変分原理)
摂動法よりもさらに広い範囲で用いられている近似法に変分法がある。
この節では,変分法の基礎になる変分原理を解説した後,ヘリウム原子の基底状態エネルギーの計算に変分法を応用する。
(副読本 pp. 114〜128)
Schr dinger 方程式
dinger 方程式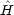
 = E
= E で, E0 を最低固有値,
で, E0 を最低固有値,  0 を対応する固有関数とするとき,任意の関数
0 を対応する固有関数とするとき,任意の関数  について次の関係が成立する。(変分原理)
について次の関係が成立する。(変分原理)
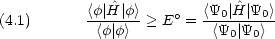
 i は規格完全直交系をなすので
i は規格完全直交系をなすので 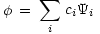 と書くことが出来る。
と書くことが出来る。
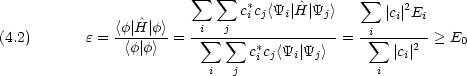
厳密には解けないような Schr dinger 方程式に対して変分原理を適用するのが,変分法とよばれる近似法である。
dinger 方程式に対して変分原理を適用するのが,変分法とよばれる近似法である。
つまり,試行関数として適当な形を選び,エネルギー期待値が最小になるようにパラメータを決めることによって,現実に近いエネルギーと波動関数を求めようとするものである。
試行関数がよければ非常に現実に近い結果が得られるが,一般にはどんな関数形がよいかがわからない場合も多い。
厳密解と同じ形の関数を用いれば,エネルギーは厳密解と一致する。しかし,おかしな試行関数を仮定すると計算不可能なこともある。
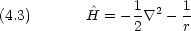
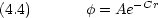
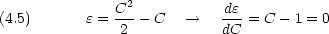
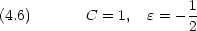
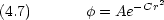
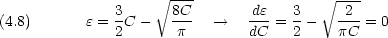
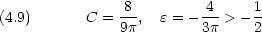
原子核の電荷数を Z とする。原子単位を用いる
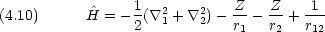
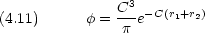
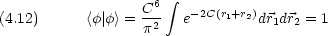
 を求める計算で,ハミルトニアンの中の核電荷は Z だが,試行関数では有効核電荷 C を用いることに注意する
を求める計算で,ハミルトニアンの中の核電荷は Z だが,試行関数では有効核電荷 C を用いることに注意する
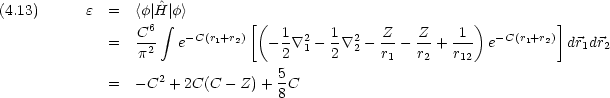
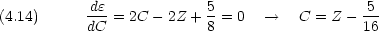
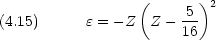
ヘリウムの基底状態エネルギーの数値計算結果 (eV)
|
無摂動
|
変分法
|
一次摂動
|
実験値
|
|
| He |
-108.24
|
-77.06
|
-74.42
|
-78.62
|
 = Ae-Cx2
= Ae-Cx2
 = Ae-C|x|
= Ae-C|x|
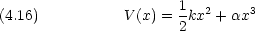
 は正の定数で,
は正の定数で,  の絶対値は小さいものとする。
の絶対値は小さいものとする。

 は正の定数である。次の関数を試行関数とした変分法によって基底状態エネルギーを計算せよ。
は正の定数である。次の関数を試行関数とした変分法によって基底状態エネルギーを計算せよ。

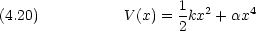
 は正の定数で,
は正の定数で,  の絶対値は小さいものとする。
の絶対値は小さいものとする。
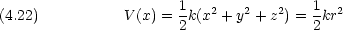






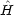 とし,試行関数を次の形に置く。
とし,試行関数を次の形に置く。
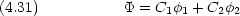
 1 と
1 と  2 は一次独立な関数である。 C1 と C2 とをパラメータとした変分法で基底状態エネルギーを計算する。
2 は一次独立な関数である。 C1 と C2 とをパラメータとした変分法で基底状態エネルギーを計算する。
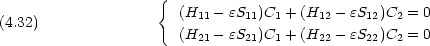
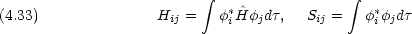
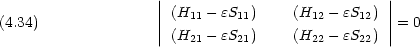
 1 と
1 と  2 が規格化されており,かつ直交しているとき, (1) 及び (2) の方程式はどのようになるか。
2 が規格化されており,かつ直交しているとき, (1) 及び (2) の方程式はどのようになるか。
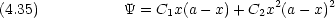
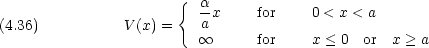
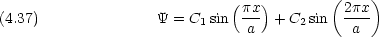
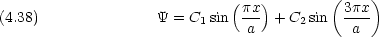
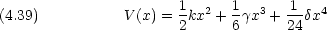
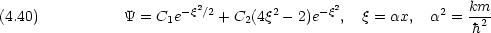
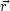 とすると,双極子モーメント
とすると,双極子モーメント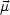 は-e
は-e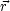 で与えられる。
で与えられる。

 1s は 1s 軌道,
1s は 1s 軌道,  2pz は 2pz 軌道の波動関数である。答えは次のようになる。
2pz は 2pz 軌道の波動関数である。答えは次のようになる。
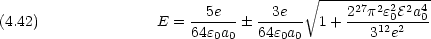
 0 は真空の誘電率, a0 は Bohr 半径である。
0 は真空の誘電率, a0 は Bohr 半径である。
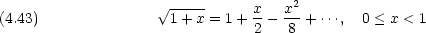
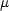 は電場E に比例する。
は電場E に比例する。

 を分極率という。電場によって双極子モーメント
を分極率という。電場によって双極子モーメント 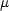 を誘起するのに必要なエネルギーはどれだけか。次の積分によって見積もれ。
を誘起するのに必要なエネルギーはどれだけか。次の積分によって見積もれ。

 2pz の代わりに
2pz の代わりに  3pz を使った場合,結果はどう変わるか。
3pz を使った場合,結果はどう変わるか。