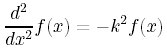変数分離の部分（ 8 章 ）などを参照してもらえればわかるこの式が出発点となる。
この章で、「猫でもわかる量子力学」もおしまい。ということで今までの総決算をする。
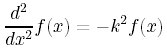変数分離の部分（ 8 章 ）などを参照してもらえればわかる
この式が出発点となる。
Louis Victor de Broglie (1892〜1987)
X線の実験的研究を進めていた兄C.M.de Broglie（1875〜1960）に触発され、
という新しいアイデアを提案。
1924年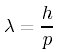
（λ：電子波の波長、h：プランク定数、p：運動量）を導いた。
1929年 ノーベル 物理学賞を受賞。
参考URL：ド・ブロイのデータ
なので（角周波数の定義） de Broglie波を代入すると
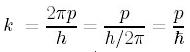となる。ちなみに
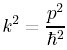を１に代入。
 |
；運動エネルギー部分
：ポテンシャル（位置エネルギー）
運動量
なので、
これをEに代入する。
これをpについて解くと、
となる。これを
|
に代入すると
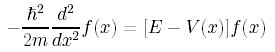この式を整理すると
 |
この式を、量子力学的波動関数 
方程式という。
以降、物理化学V・Wの諸問題はすべてこの方程式を出発点とする。
…この式を導くために、今まで「猫でもわかる量子力学」をといてもらっていたのです。お疲れ様。
