第７章　波の速さ

はじめに見てほしいのが上のFlashだ。

波は x 軸について + の方向に進んでいく。
そして，t = 0 の時の波の形を f(x) とし、 t = 0 の時，
波の中で頂上だったところを x = a とすると
頂上の位置は t = t になれば x = a + vt に移動している。
でも，f(x)は，t 含んでいないので頂上の場所はいつまでたっても x = a になる。
つまり，x = a + vt になってしまった時点で考えれば，x - vt = a となる。

ここで、t=0のときのオリジナル波形をf(x)と置く。

すると、t = tのときの波形はf(x-vt)とあらわすことができる。

つまり、ｘとｔは別々ではなく、必ず(x-vt)という組になって現れる関数なのである。

これを、古典的波動方程式の形にするにはどうしたらいいだろうか。古典的波動方程式は 6章 でも出てきたとおり、xとtの2階微分が必要である。
…答えは「右辺と左辺を別々に求める」　そうすることによって、両方の2階微分を得ることができる。

さて。とおき、式を変形していこう。（Zをｘで微分したら、またtで微分したらどうなるか…は、OKだね？）

とする。

まず、ｘの１階微分から。

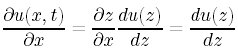
２階微分は

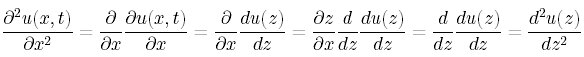
それで、ｔの１階微分は

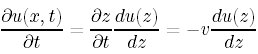
ｔの2階微分は

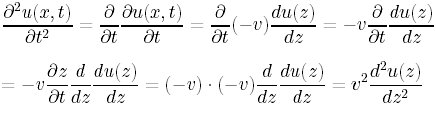
めでたく両方とも2階微分できたところで波動方程式に代入しよう。

ということで、両辺から2階微分のパートを消して
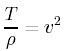つまり、波の速さｖは
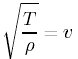このように張力と線密度により導くことができる。

ｖをつかって波動方程式を書き直すと

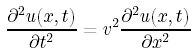
これを、一般の古典的波動方程式と呼んでいる。