5章 で、下向きに働く力は
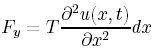 と結論付けることができた。また5章の問題で、
と結論付けることができた。また5章の問題で、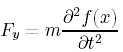 とも表せることがわかる。(先回りして、答えを見た人へ; F = ma 思い出した?)
とも表せることがわかる。(先回りして、答えを見た人へ; F = ma 思い出した?)さて、mは質量だが、質量は「線密度(単位長さあたりの質量)×長さ」であらわすことができる。
これを代入していこう。
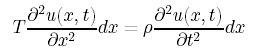
両辺にdxがあるので、これを消すと
さて、この章ではいままでの「波の運動」の総大成だ。
5章 で、下向きに働く力は
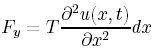 と結論付けることができた。また5章の問題で、
と結論付けることができた。また5章の問題で、
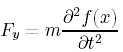 とも表せることがわかる。(先回りして、答えを見た人へ; F = ma 思い出した?)
とも表せることがわかる。(先回りして、答えを見た人へ; F = ma 思い出した?)
さて、mは質量だが、質量は「線密度(単位長さあたりの質量)×長さ」であらわすことができる。
![]() この式のρ(ロー、と読む。英語ではrhoと書く)が線密度で、dxが長さ。
この式のρ(ロー、と読む。英語ではrhoと書く)が線密度で、dxが長さ。
これを代入していこう。
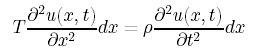
両辺にdxがあるので、これを消すと
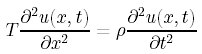
|
これを、「古典的波動方程式」と呼ぶ。
左辺の2回微分は湾曲のパラメータ、
右辺の2回微分は加速度を表し、力のかかっていることをあらわしている。