第５章　波の運動　その２

さて、次は弦のたわみについて、もっと微小な視点から見ていこう。 左の図を見てほしい。赤はφの直線を、青はsinφの曲線をあらわしている。 φの値が大きくなればなるほど、両者の差は大きくなっていくが、もしφがとても小さい値であったとき、両者に差はほとんど見られない。 つまり、角度φがとても小さな値であったとき、 という式があてはまる。

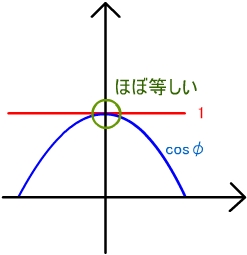
同じことを、今度はcos についても考えてみる。cosφと1の値は、φの値が小さくなればなるほどほとんど差がなくなってくる。 cos0 = 1という式を覚えている人も多いと思うけど、0に近くなればなるほど1に近くなるのは当たり前のことだね。 cos に関しても、角度φがとても小さな値であったとき という式が当てはまる。

ところで、式に出ているだけれども、これは「ほぼ等しい」という意味で、この３つは同じ意味を持つ。
3番目のやつは、高校の数式でもおなじみだね。物理化学の時間ではを用いるので混乱のないよう。

さて。上記の２つを踏まえて、式を変形していこう。

つまり、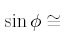 と書き表すことができる。

さて。ここから 4章 で考えた下向きの力について解いていこう。
今、波の関数をf(x)とする。f(x)とは、y=0の位置からどれだけ弦が動いたのかをxを用いてあらわしたもの。つまり、y軸での変化だね。

高校の時に出てきた式として、
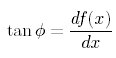という式があるけれども、それを応用しよう。

4章の図を、もう一度載せておく。

4章 で出題した、下向きの力は
と表すことができる。 sinはtanに変換することが可能になったので
とかける。

ここで、φはx = x+dx, θはx = xの時の弦の角度であったので（２つの変数が１つで表示できるところがＰＯＩＮＴ）
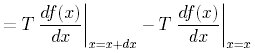となる。１階積分をf'(x)と表すことにすると
となる。

本来、dxは微小な領域で（上の図ではえらいデカクなっているが）、本来、dx→0の極限の状態を考えないといけない。
この式のTにdxをかけ、極限の部分をdxで割ってみよう

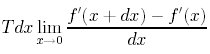
さて、微分の定義から、
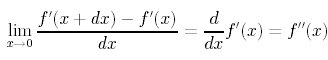ということができる。
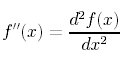と書くことができるから、結局
と書くことができるわけだ。

問題　：　高校のときに習ったNewtonの第２法則を覚えているだろうか。 　　　　　今回の問題は、それがヒント。 　　　　　u(x,t) が，ある瞬間 t = t で， x = x における y 方向への変位であるとする。 　　　　　（つまり上の式で、ｆ が u に置き換わったと思ってほしい） 　　　　　弦にかかる力は次のどの式で表せるだろうか。　　　　但し、m は弦の質量を表す。