最平坦特性を持つ低域通過梯子型回路の規格化素子値
低域通過梯子型回路は双対的な次のような回路で表され，\(N\)次の最平坦特性を有する梯子型リアクタンス回路を合成すると，規格化素子値\(g_k\)は，次のようになる．
\begin{eqnarray}
g_0 &=& 1\\
g_k &=& 2 \sin \left( \frac{(2k-1) \pi }{2N} \right)
\ \ \ (k=1,2, \cdots ,N)\\
g_{N+1} &=& 1
\end{eqnarray}
ただし，\(g_0\)は入力の負荷抵抗，\(g_{N+1}\)は終端負荷の抵抗を示す．
入力インピーダンス\(z_{in}^+\)により合成した梯子型回路
入力インピーダンス\(z_{in}^-\)により合成した梯子型回路
最平坦特性を有する低域通過フィルタの規格化素子値\(g_k\)を求めると次のようになる．
\begin{array}{c|cccccccc}
\hline
N & g_1 & g_2 & g_3 & g_4 & g_5 & g_6 & g_7 & g_8\\
\hline \hline
1 & 2 & 1 &{} & {} & {} & {} & {} & {} \\
\hline
2 & \sqrt{2} & \sqrt{2} & 1 & {} & {} & {} & {} & {} \\
\hline
3 & 1 & 2 & 1 & 1 & {} & {} & {} & {} \\
\hline
4 & 0.7654 & 1.8478 & 1.8478 & 0.7654 & 1 & {} & {} & {} \\
\hline
5 & 0.6180 & 1.6180 & 2 & 1.6180 & 0.6180 & 1 & {} & {} \\
\hline
6 & 0.5176 & \sqrt{2} & 1.9318 & 1.9318 & \sqrt{2} & 0.5176 & 1 & {} \\
\hline
7 & 0.4450 & 1.2470 & 1.8019 & 2 & 1.8019 & 1.2470 & 0.4450 & 1 \\
\hline
\hline
\end{array}
これより，\(N=2,3,4, 5\)について入力インピーダンス\(z_{in}^+\)で合成した回路の特性を求めると次のようになる．
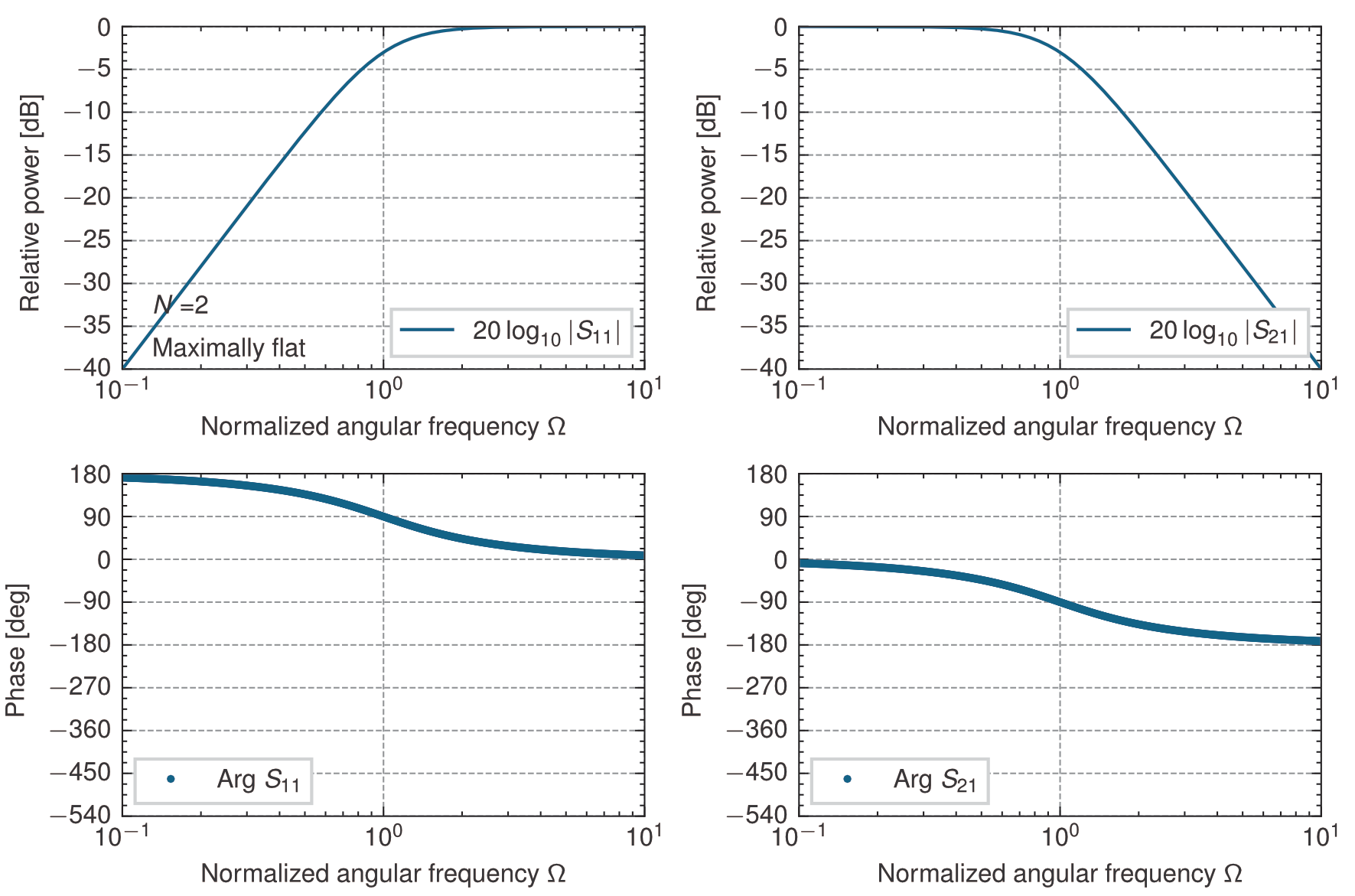2段梯子型回路の低域通過特性（入力インピーダンス\(z_{in}^+\)）
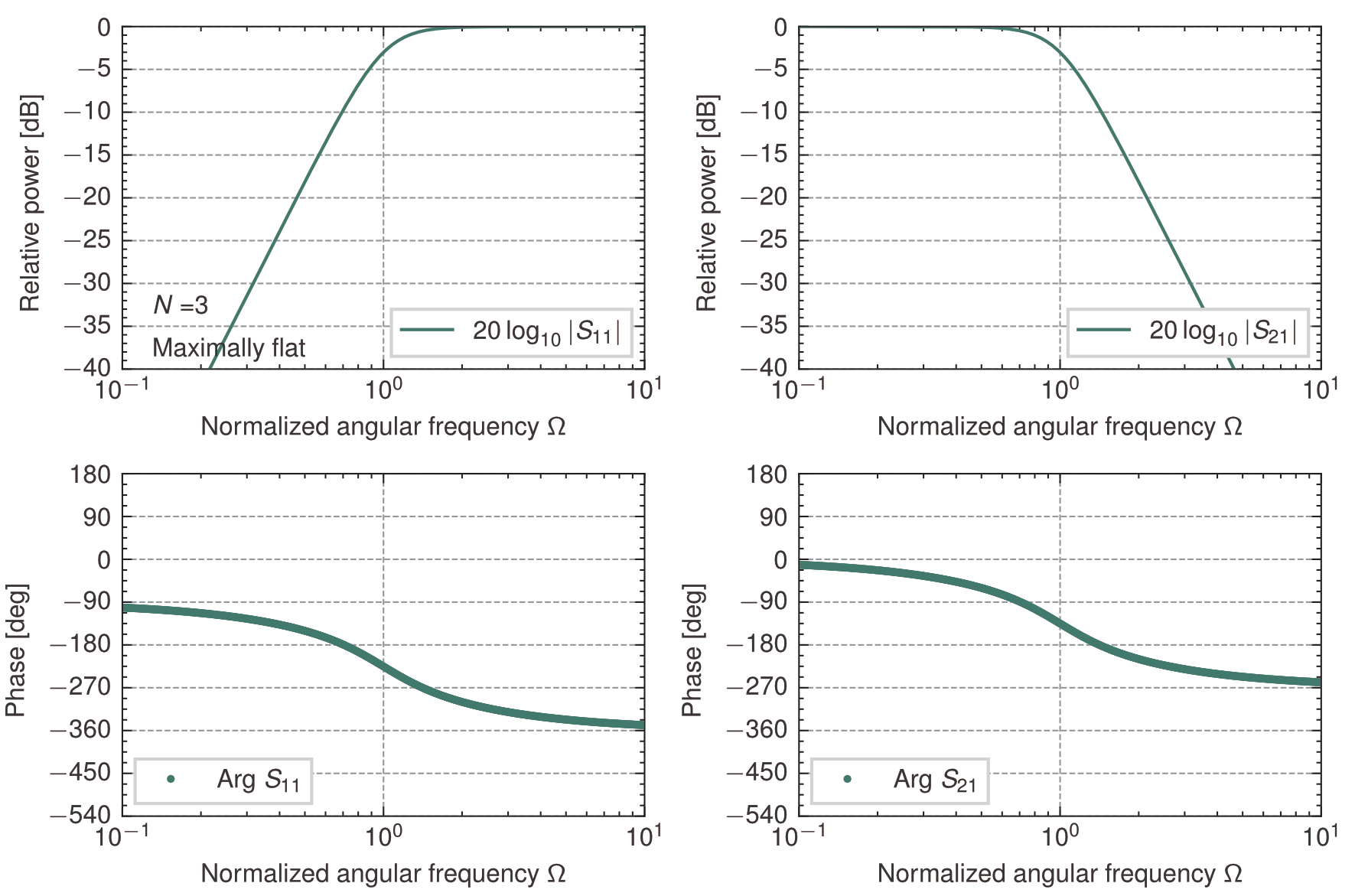3段梯子型回路の低域通過特性（入力インピーダンス\(z_{in}^+\)）
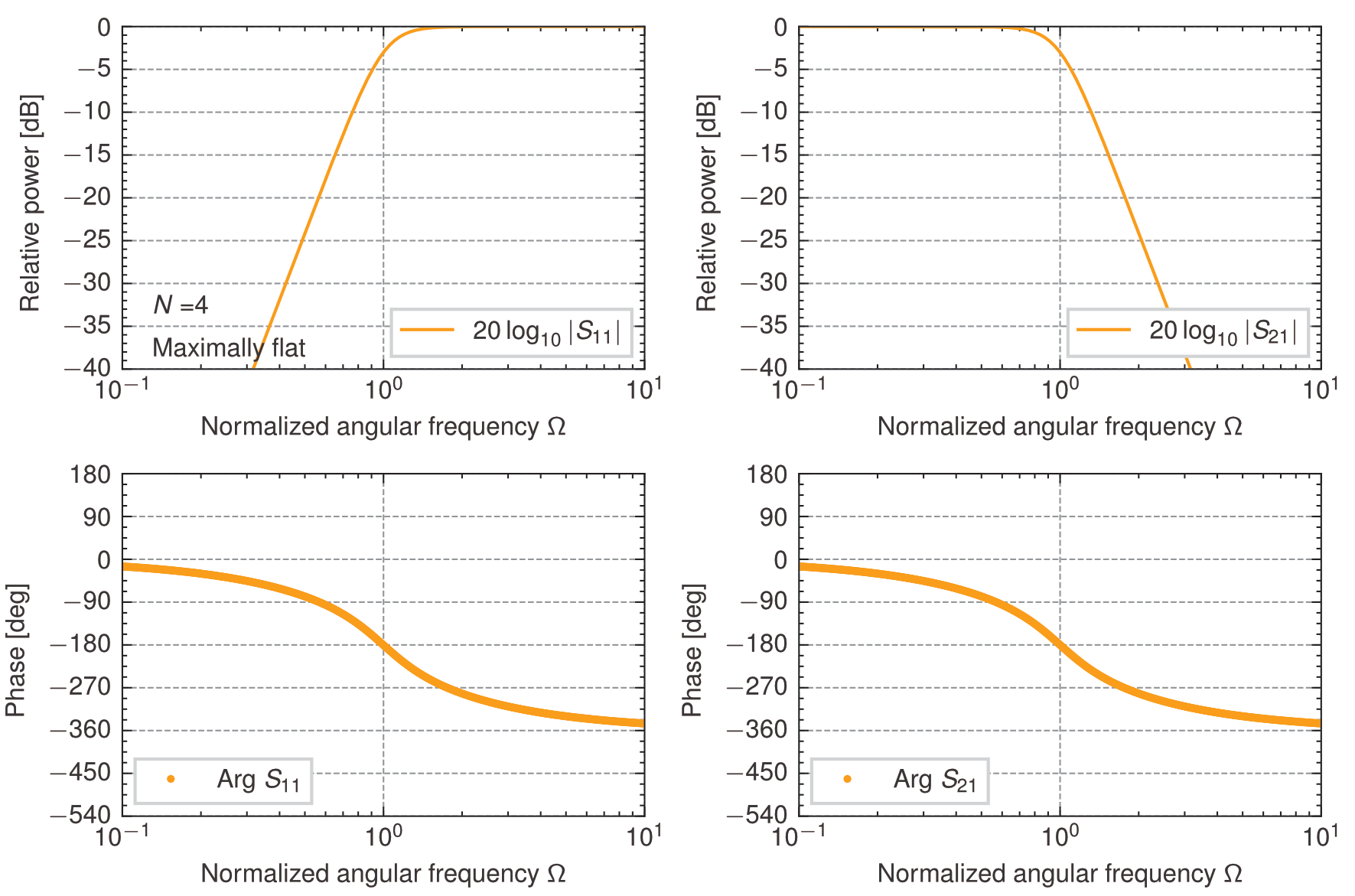4段梯子型回路の低域通過特性（入力インピーダンス\(z_{in}^+\)）
5段梯子型回路の低域通過特性（入力インピーダンス\(z_{in}^+\)）