周波数変換により求めた等リプル特性を持つ高域通過梯子型回路の規格化素子値
高域通過フィルタは，周波数変換\(s=\frac{1}{\hat{s}}\)より，梯子型回路の直列素子の規格化インピーダンス\(z_k\)，並列素子の規格化アドミタンス\(y_k\)は（入力の抵抗は1），
\begin{gather}
z_k = s g_k = \frac{g_k}{\hat{s}} \equiv \frac{1}{\hat{s} \hat{g}_k} = \frac{1}{\hat{y}_k}\\
y_k =s g_k = \frac{g_k}{\hat{s}} \equiv \frac{1}{\hat{s} \hat{g}_k} = \frac{1}{\hat{z}_k}
\end{gather}
よって，高域通過フィルタの規格化素子値\(\hat{g}_k\)は，
\begin{gather}
\hat{g}_k = \frac{1}{g_k}
\end{gather}
高域通過梯子型回路は双対的な次のような回路となる．
\(z_{in}^+\)により合成した原型低域通過回路を周波数変換した高域通過梯子型回路
\(z_{in}^-\)により合成した原型低域通過回路を周波数変換した高域通過梯子型回路
等リプル（0.04365 dB）特性を有する高域通過フィルタの規格化素子値\(\hat{g}_k\)を求めると次のようになる．
ただし，入力抵抗\(g_0 =1\)，終端負荷の素子値は$N$が奇数のとき\(g_{N+1}=1\)，\(N\)が偶数のとき\(g_{N+1} \big|_{L_{Ar}=0.04365}=1.2222\)．
このとき，通過域の反射のピーク値は\(-20\)dB．
\begin{array}{c|cccccccc}
\hline
N & \hat{g}_1 & \hat{g}_2 & \hat{g}_3 & \hat{g}_4 & \hat{g}_5 & \hat{g}_6 & \hat{g}_7\\
\hline \hline
2 & 1.5000 & 1.8333 \\ \hline
3 & 1.1717 & 0.9059 & 1.1717 \\ \hline
4 & 1.0715 & 0.7738 & 0.6331 & 1.3097 \\ \hline
5 & 1.0275 & 0.7287 & 0.5546 & 0.7287 & 1.0275 \\ \hline
6 & 1.0042 & 0.7076 & 0.5277 & 0.6450 & 0.5790 & 1.2274 \\ \hline
7 & 0.9903 & 0.6960 & 0.5151 & 0.6167 & 0.5151 & 0.6960 & 0.9903 \\ \hline
\hline
\end{array}
これより，\(N=2,3,4,5,6,7\)について入力インピーダンス\(z_{in}^+\)で回路合成し，
偶数次\(N=2,4,6\)については終端に理想変成器を追加して周波数応答を求めると次のようになる．
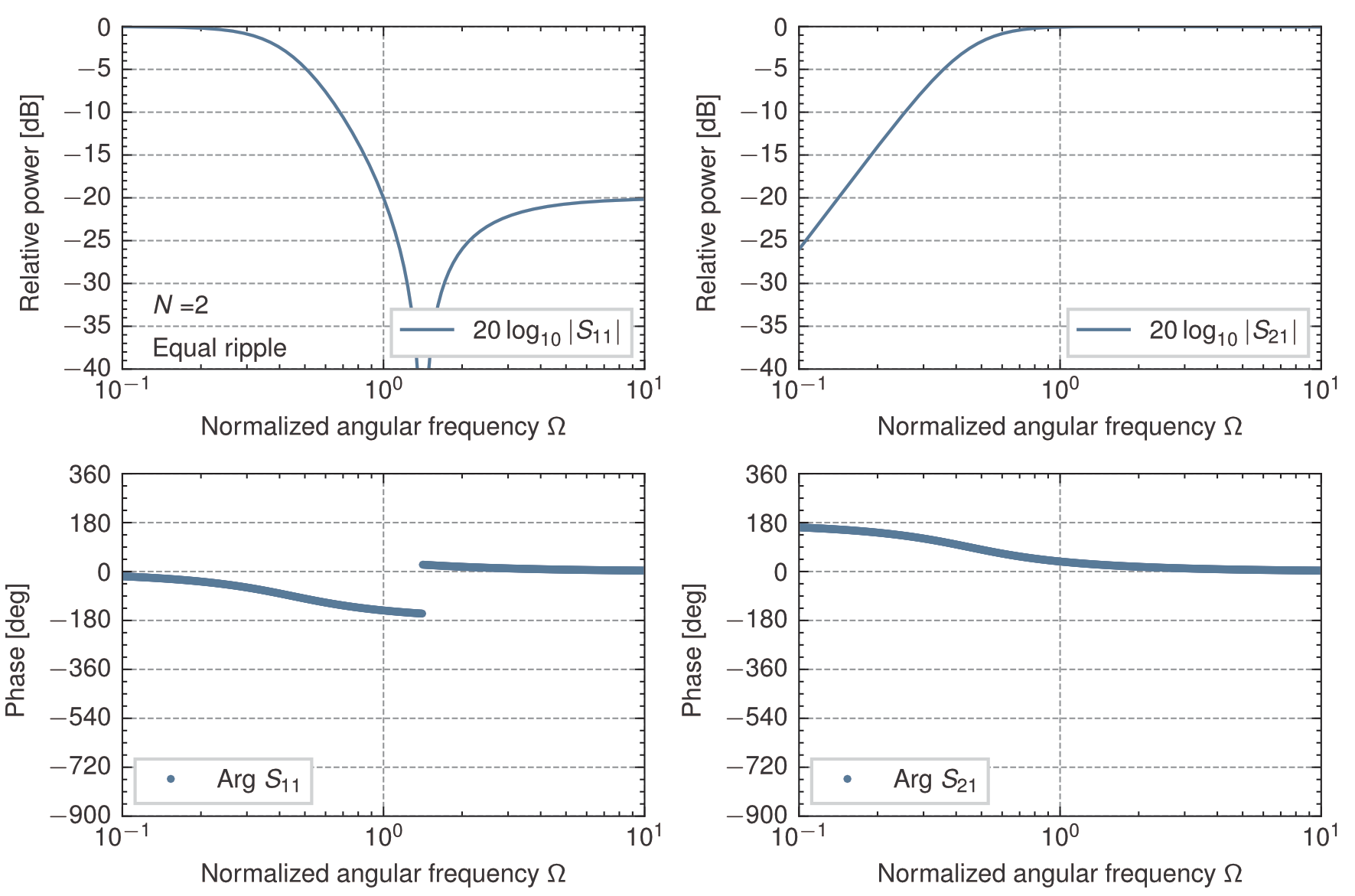理想変成器を接続した2段梯子型回路の\(0.04365\)dB（反射=\(-20\)dB）等リプル高域通過特性（\(z_{in}^+\)）
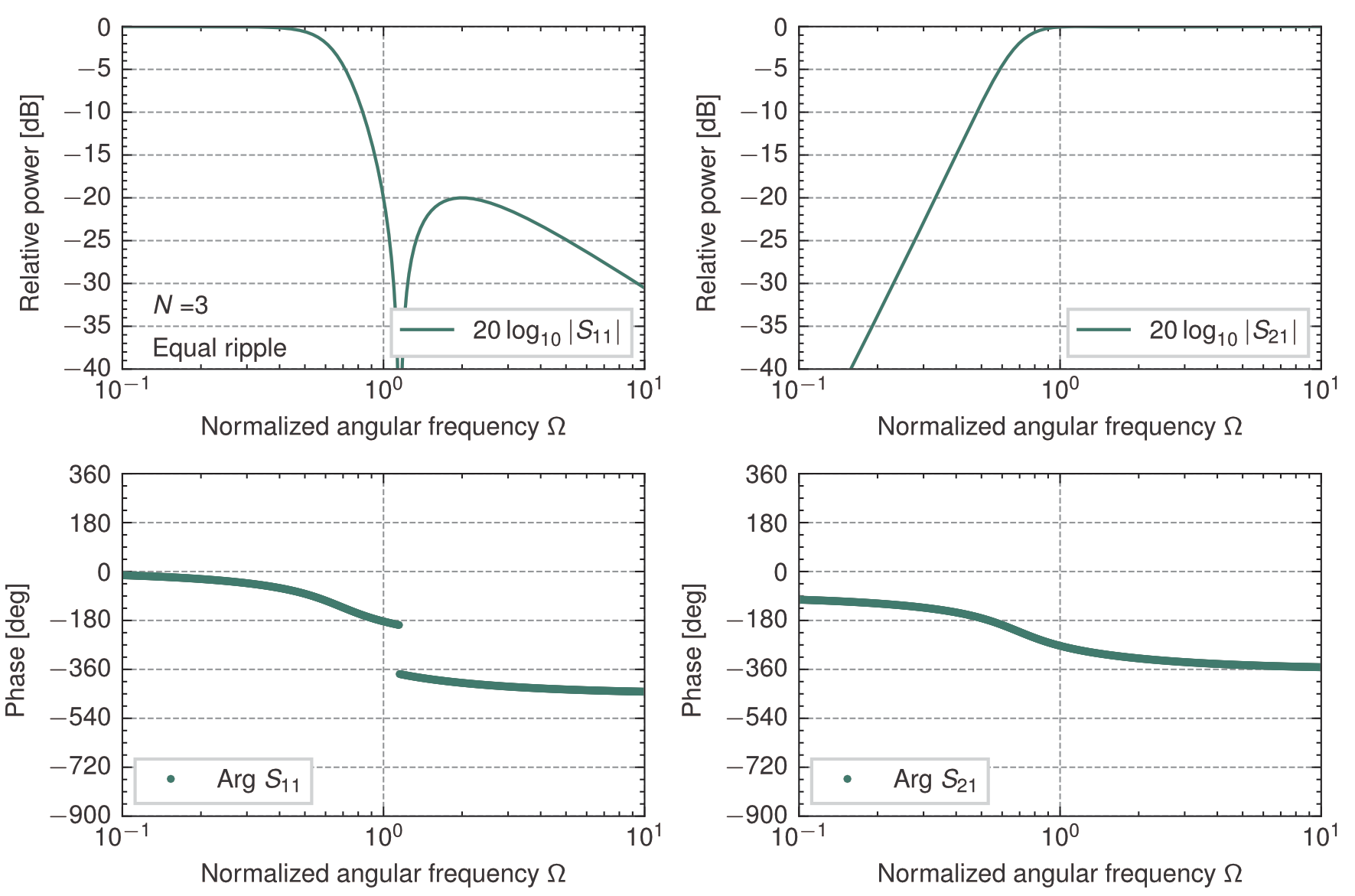3段梯子型回路の\(0.04365\)dB（反射=\(-20\)dB）等リプル高域通過特性（\(z_{in}^+\)）
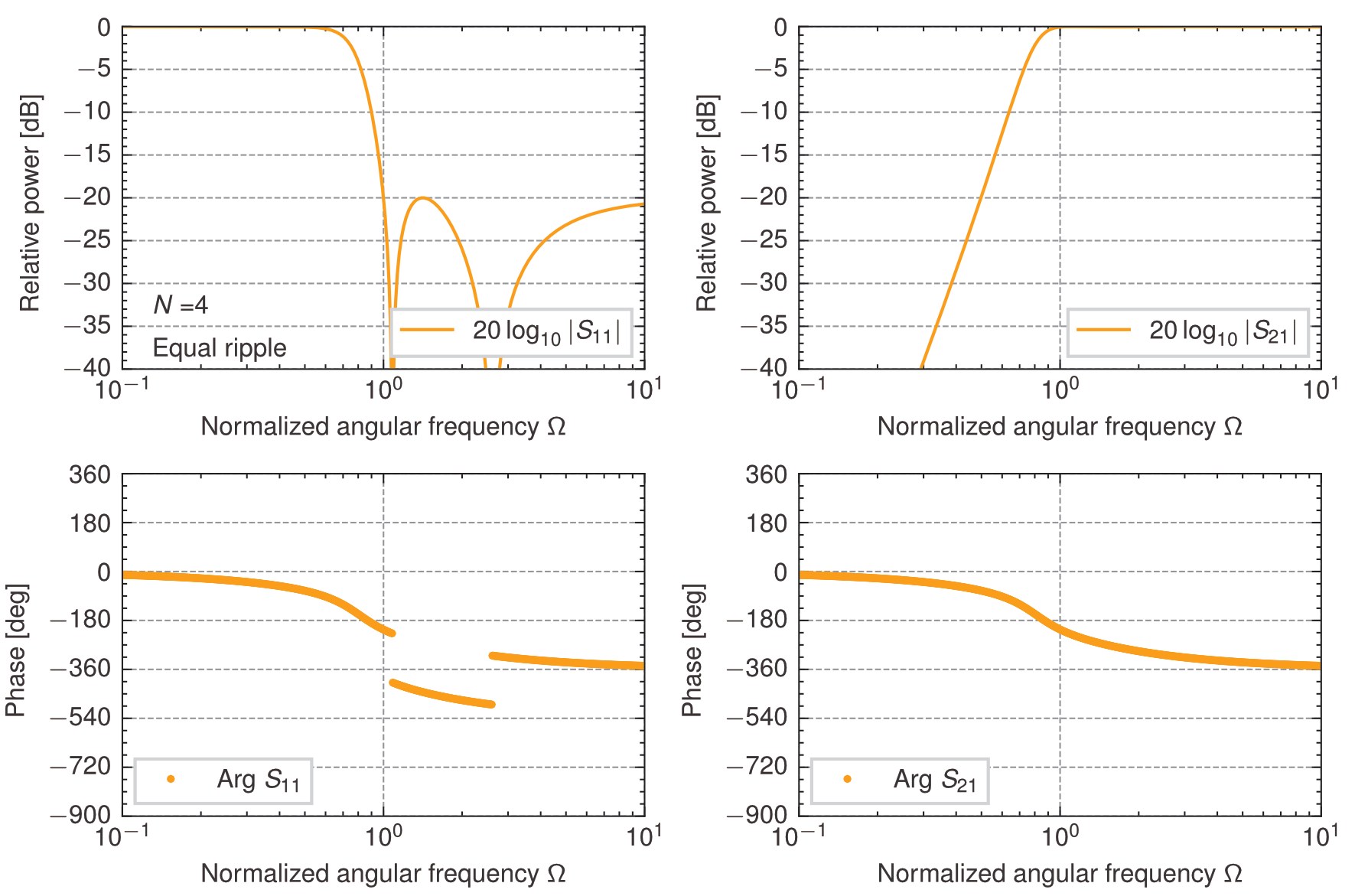理想変成器を接続した4段梯子型回路の\(0.04365\)dB（反射=\(-20\)dB）等リプル高域通過特性（\(z_{in}^+\)）
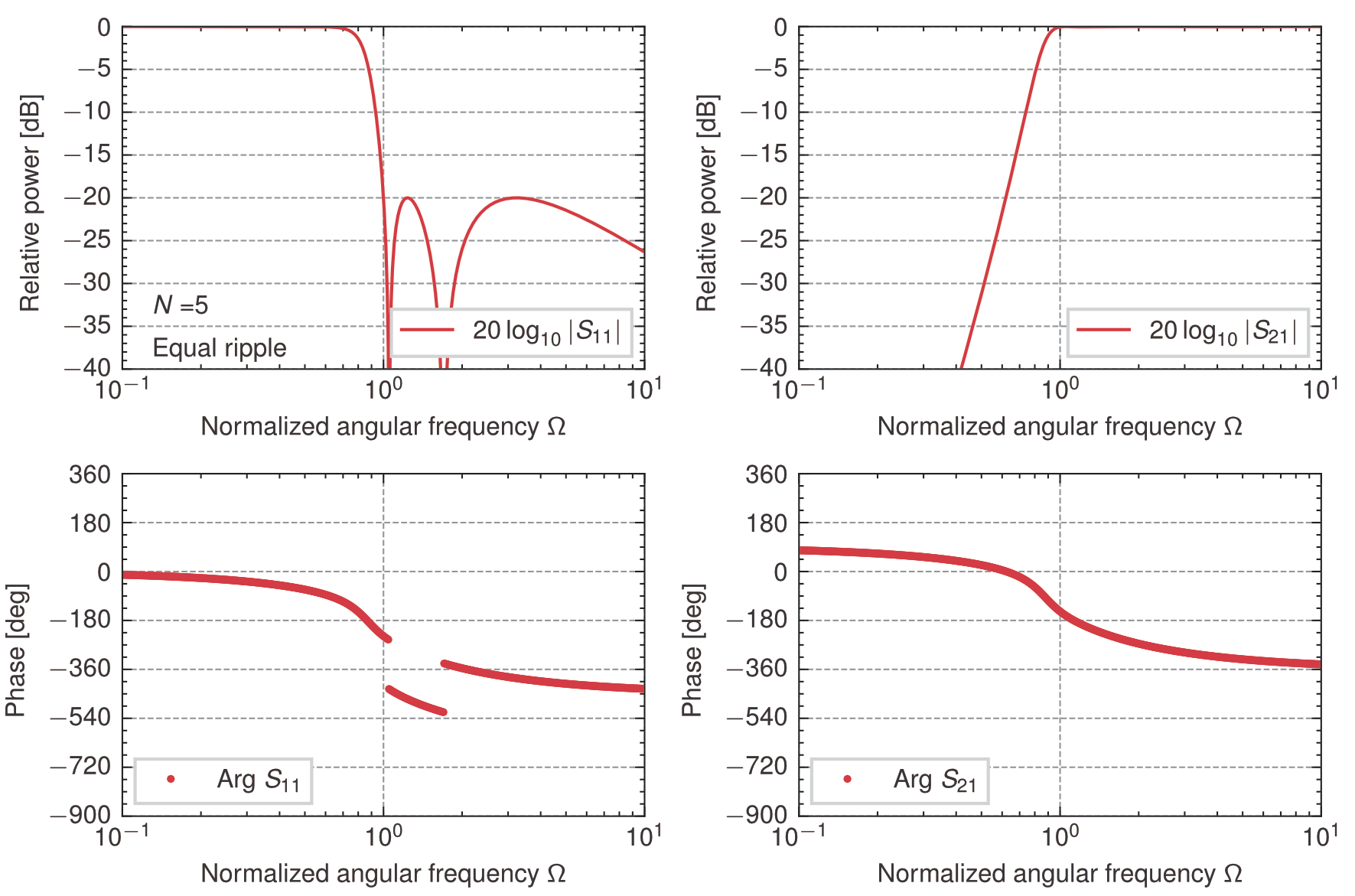5段梯子型回路の\(0.04365\)dB（反射=\(-20\)dB）等リプル高域通過特性（\(z_{in}^+\)）
理想変成器を接続した6段梯子型回路の\(0.04365\)dB（反射=\(-20\)dB）等リプル高域通過特性（\(z_{in}^+\)）
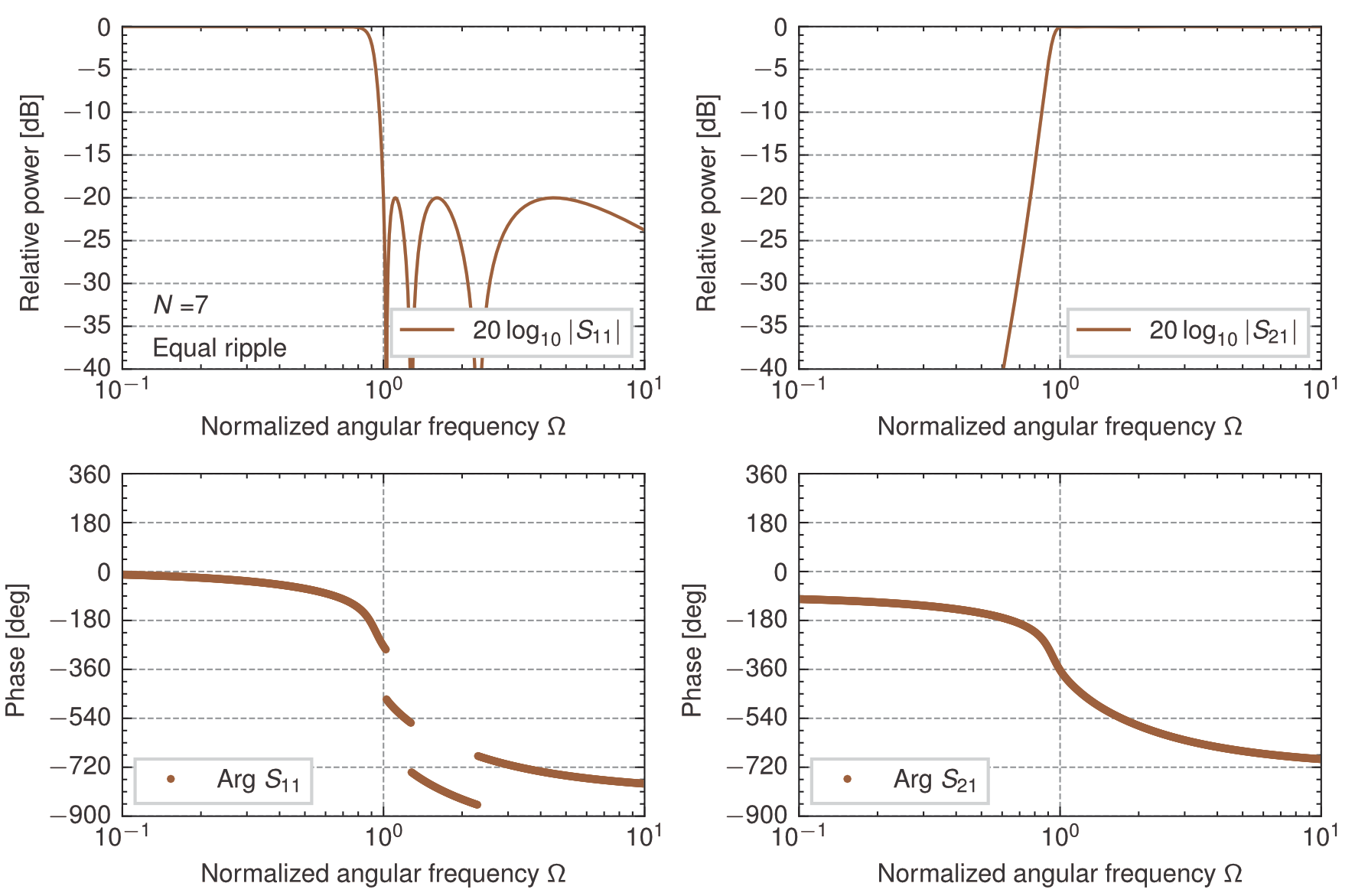7段梯子型回路の\(0.04365\)dB（反射=\(-20\)dB）等リプル高域通過特性（\(z_{in}^+\)）