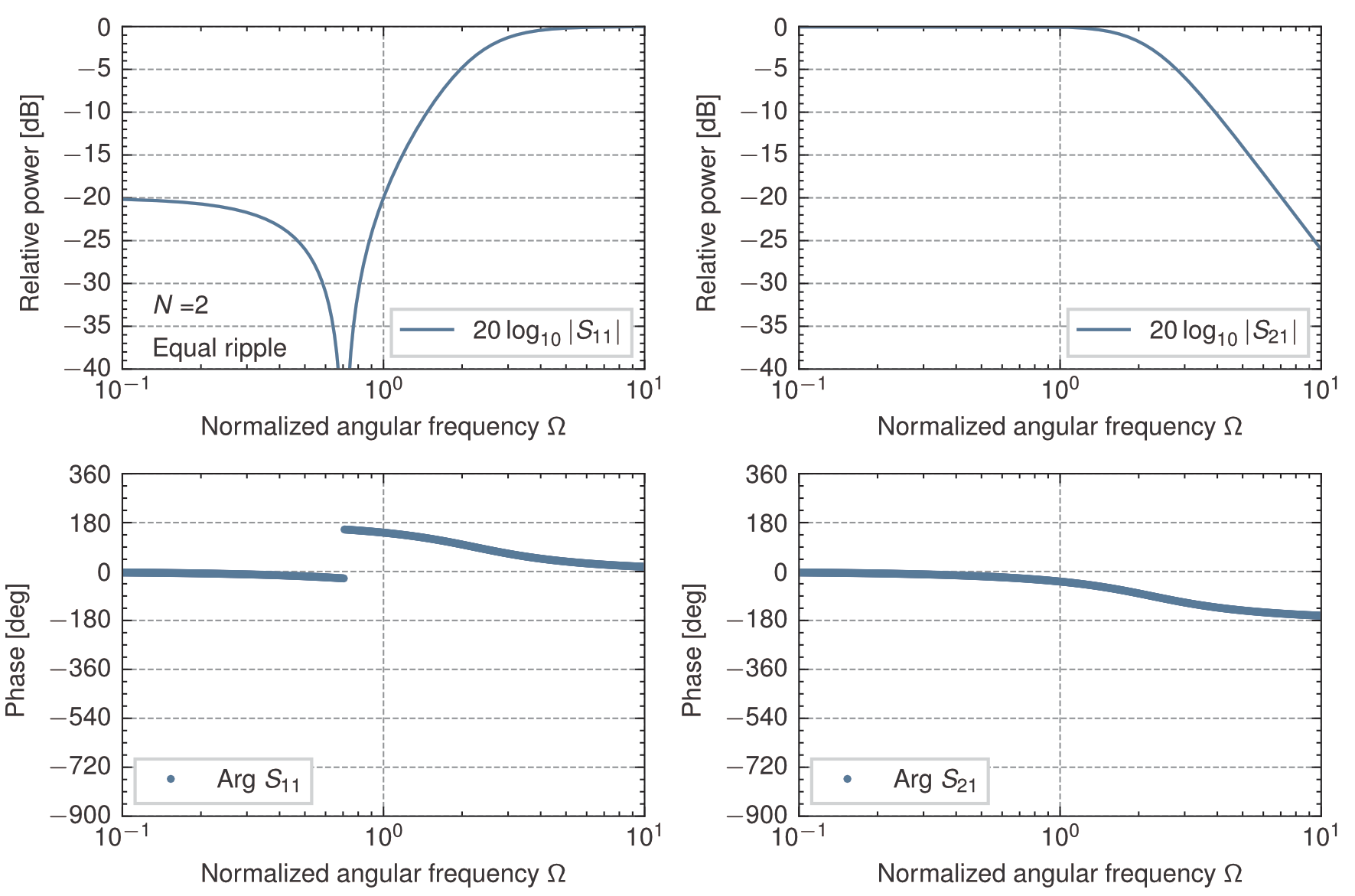
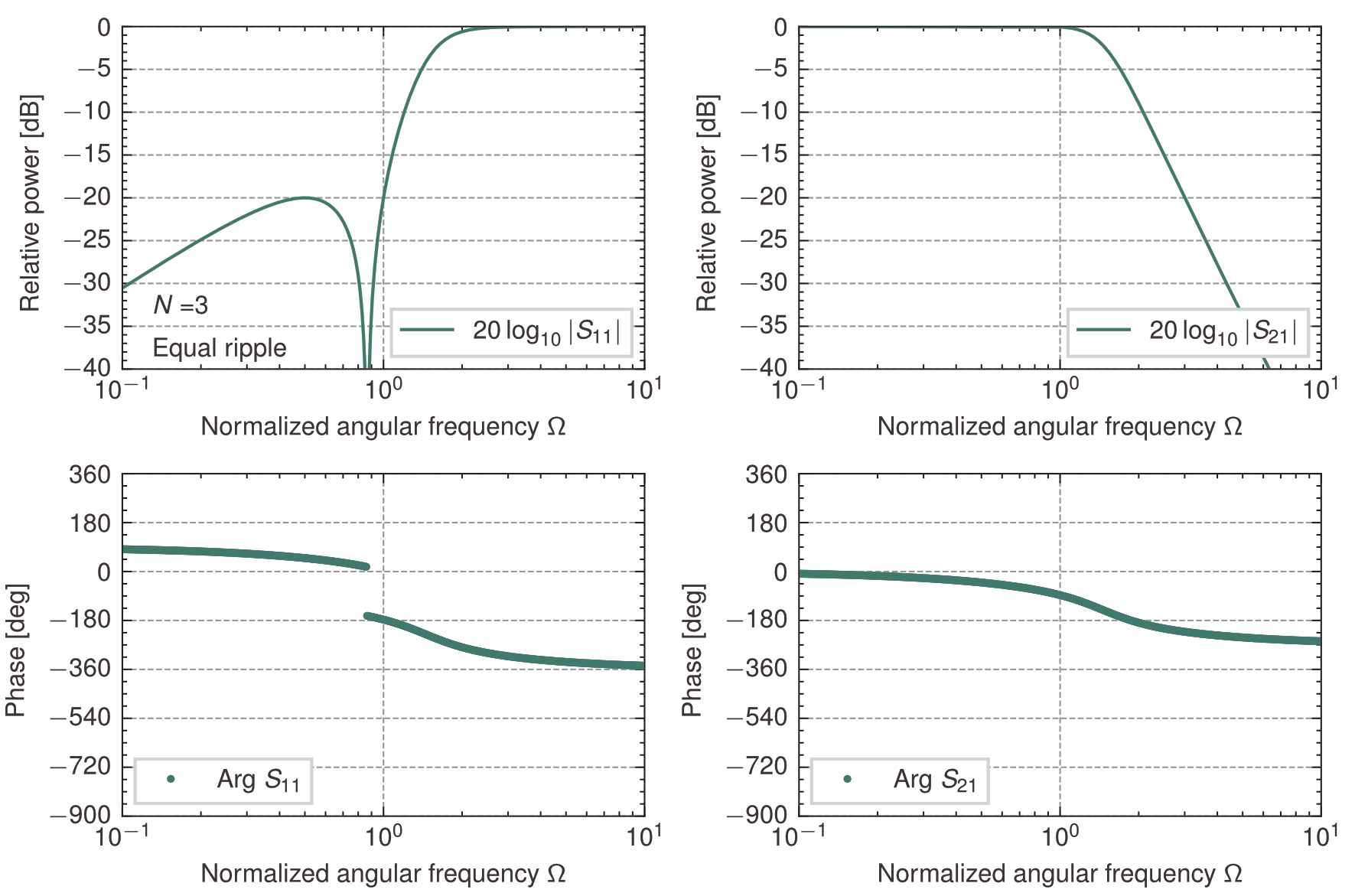
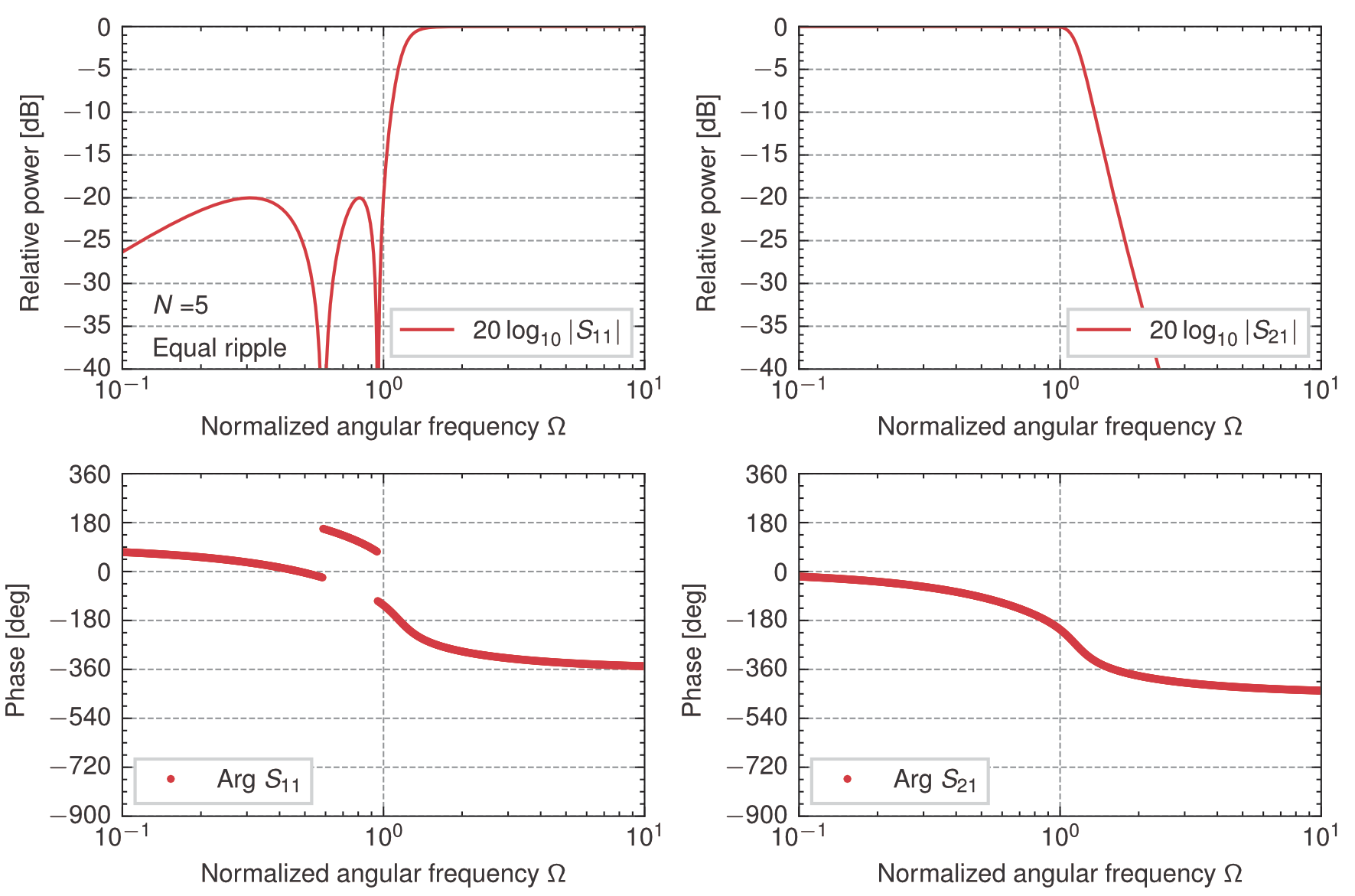
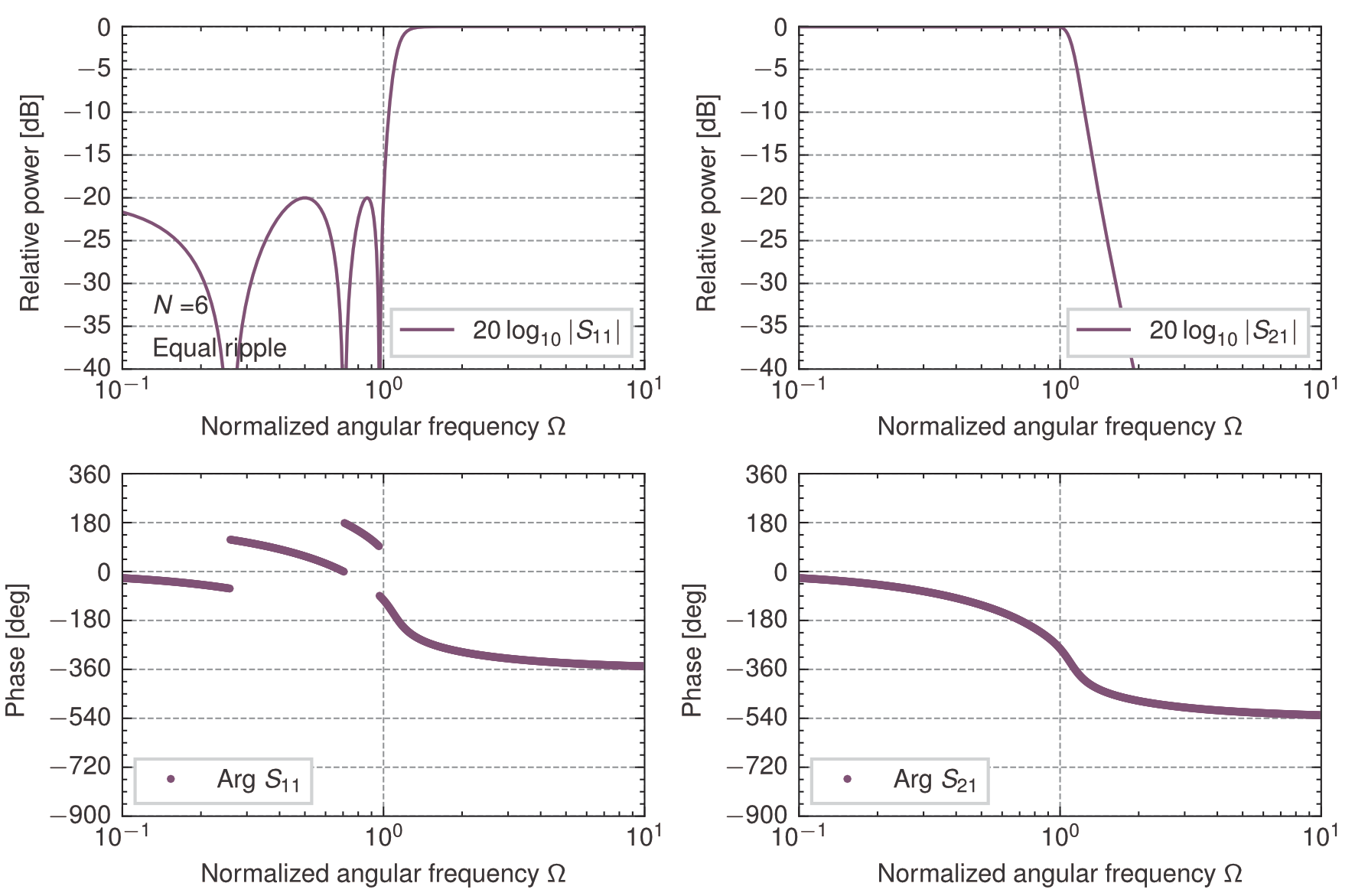
等リプル(0.04365 dB)を有する低域通過フィルタの規格化素子値\(g_k\)を求めると次のようになる. ただし,\(g_0 =1\),終端負荷の素子値は$N$が奇数のとき\(g_{N+1}=1\),\(N\)が偶数のとき\(g_{N+1} \big|_{L_{Ar}=0.04365}=1.2222\). このとき,通過域の反射のピーク値は\(-20\)dBである.
\begin{array}{c|cccccccc} \hline N & g_1 & g_2 & g_3 & g_4 & g_5 & g_6 & g_7 & g_8\\ \hline \hline 2 & 0.6667 & 0.5455 & 1.2222 \\ \hline 3 & 0.8535 & 1.1039 & 0.8535 & 1.0000 \\ \hline 4 & 0.9333 & 1.2923 & 1.5795 & 0.7636 & 1.2222 \\ \hline 5 & 0.9732 & 1.3723 & 1.8032 & 1.3723 & 0.9732 & 1.0000 \\ \hline 6 & 0.9958 & 1.4131 & 1.8950 & 1.5505 & 1.7272 & 0.8148 & 1.2222 \\ \hline 7 & 1.0097 & 1.4368 & 1.9414 & 1.6216 & 1.9414 & 1.4368 & 1.0097 & 1.0000 \\ \hline \hline \end{array} 奇数次のチェビシェフ特性の場合,梯子型回路の終端負荷は\(g_{N+1} =1\)であるのに対し,偶数次の場合,終端負荷は\(g_{N+1} \ne 1\)であるが,両者ともに各々の負荷に対して所定の伝送特性が得られる. 当然,偶数次の回路に\(r = 1\)の終端負荷を接続しても所定の特性は得られない. しかしながら,梯子型回路と終端負荷の間に理想変成器(\(n : 1\))を挿入して,梯子型回路から変成器(終端負荷は\(r=1\))を見た規格化入力インピーダンス(梯子型回路の最終段が並列素子の場合),あるいは規格化入力アドミタンス(最終段が直列素子の場合)を\(g_{N+1}\)とすれば,所定の特性を得ることができる. 梯子型回路の最終段が並列素子の場合,規格化入力インピーダンス\(z_{in} = g_{N+1}\)となるように, \begin{eqnarray} z_{in} &=& \frac{V_1}{I_1} = \frac{nV_2}{\frac{-1}{n}I_2} = n^2 \frac{V_2}{-I_2} \nonumber \\ &=& n^2 = g_{N+1} \end{eqnarray} よって,\(n = \sqrt{g_{N+1}}\)ゆえ,理想変成器の入出力端子の電圧,電流の関係は次のようになる. \begin{eqnarray} \begin{pmatrix} V_1 \\ I_1 \end{pmatrix} &=& \begin{pmatrix} n & 0 \\ 0 & \frac{1}{n} \\ \end{pmatrix} \begin{pmatrix} V_2 \\ -I_2 \end{pmatrix} \nonumber \\ &=& \begin{pmatrix} \sqrt{g_{N+1}} & 0 \\ 0 & \frac{1}{\sqrt{g_{N+1}}} \\ \end{pmatrix} \begin{pmatrix} V_2 \\ -I_2 \end{pmatrix} \end{eqnarray} 梯子型回路の最終段が直列素子の場合,規格化入力アドミタンスが\(y_{in} = g_{N+1}\)となるように, \begin{eqnarray} \frac{1}{y_{in}} &=& \frac{V_1}{I_1} = \frac{nV_2}{\frac{-1}{n}I_2} = n^2 \frac{V_2}{-I_2} \nonumber \\ &=& n^2 = \frac{1}{g_{N+1}} \end{eqnarray} よって,\(n = \frac{1}{\sqrt{g_{N+1}}}\)ゆえ,理想変成器の入出力端子の電圧,電流の関係は次のようになる. \begin{eqnarray} \begin{pmatrix} V_1 \\ I_1 \end{pmatrix} &=& \begin{pmatrix} n & 0 \\ 0 & \frac{1}{n} \\ \end{pmatrix} \begin{pmatrix} V_2 \\ -I_2 \end{pmatrix} \nonumber \\ &=& \begin{pmatrix} \frac{1}{\sqrt{g_{N+1}}} & 0 \\ 0 & \sqrt{g_{N+1}} \\ \end{pmatrix} \begin{pmatrix} V_2 \\ -I_2 \end{pmatrix} \end{eqnarray} これより,\(N=2,3,4,5,6,7\)について入力インピーダンス\(z_{in}^+\)で合成した回路の特性を求めると次のようになる.