等リプル（Chebyshev）特性
チェビシェフ多項式を用いた特性関数
特性関数\(K(s)\)を，\(s = j \Omega\) より，
\begin{gather}
K(s) = K(j \Omega) \equiv \varepsilon T_N(\Omega)
\end{gather}
ここで，\(T_N(\Omega)\)は\(N\)次のチェビシェフ多項式（Chebyshev polynomial）を示し，
\begin{gather}
T_N (\Omega) = \left\{
\begin {array}{ll}
(-1)^N \cosh \big( N \cosh ^{-1} |\Omega| \big) & (\Omega < -1) \\
\cos \big( N \cos^{-1} \Omega \big) & (|\Omega| \le 1) \\
\cosh \big( N \cosh ^{-1} \Omega \big) & (\Omega > 1)
\end{array} \right.
\end{gather}
また，\(\varepsilon\) は通過域のリプルの大きさを決めるパラメータ（実数）である．これより，
\begin{eqnarray}
|K(s)|^2 &=& K(s) K(s)^*=K(s) K(-s) =K(j\Omega) K(-j\Omega)
\nonumber \\
&=& \varepsilon T_N(\Omega) \cdot \varepsilon T_N(-\Omega)
= \varepsilon^2 T_N^2(\Omega)
\\
|H(s)|^2 &=& 1+|K(s)|^2
= 1+\varepsilon^2 T_N^2 (\Omega)
\end{eqnarray}
ここで，遮断点\(\Omega =1\)のとき，\(|H|^2\)は，\(T_N(1)=1\)より，
\begin{gather}
|H|^2 \Big| _{\Omega=1} = 1+\varepsilon^2 T_N^2 (1) = 1+\varepsilon^2
\end{gather}
通過域のリプルの最大値は，
\begin{gather}
|H|_{max} = \sqrt{1+\varepsilon^2}
\end{gather}
デジベル値は，\(L_{Ar}=10 \log_{10} (1+\varepsilon^2)\) [dB]．
逆に，\(\varepsilon\)は，
\begin{gather}
\varepsilon = \sqrt{10^{\frac{L_{Ar}}{10}}-1}
\end{gather}
伝達関数の因数分解
等リプル特性\(H(s)\)を\(s\)に関して因数分解するため，\(|H(s)|^2=0\)の根を求める．\(s=j \Omega\)より，\(\Omega = -js\)ゆえ，
\begin{gather}
|H(s)|^2 = 1+\varepsilon^2 T_N^2 (-js) =0
\\
T_N^2 (-js) = - \frac{1}{\varepsilon^2}
\nonumber \\
T_N (-js) = \pm \frac{\sqrt{-1}}{\varepsilon} = \pm \frac{j}{\varepsilon}
\end{gather}
ここで，\(T_N (\Omega) = \cos ( N \cos ^{-1} \Omega )\)ゆえ，
\begin{gather}
\pm \frac{j}{\varepsilon} = \cos \{ N \cos ^{-1} (-js) \}
\end{gather}
いま，
\begin{gather}
\cos ^{-1} (-js) \equiv x+jy
\end{gather}
とおくと，加法定理および
\begin{gather}
\cos j \alpha = \cosh \alpha
\\
\sin j \alpha = j \sinh \alpha
\end{gather}
より，
\begin{eqnarray}
\pm \frac{j}{\varepsilon} &=& \cos \{ N (x+jy) \}
\nonumber \\
&=& \cos Nx \cos jNy - \sin Nx \sin jNy
\nonumber \\
&=& \cos Nx \cosh Ny - j \sin Nx \sinh Ny
\end{eqnarray}
上式の実部より，
\begin{gather}
\cos Nx \cosh Ny = 0
\end{gather}
\(\cosh Ny \ge 1\)ゆえ，\(\cosh Ny \ne 0\)．よって，\(\cos Nx =0\)が成り立つ．
したがって，\(\cos Nx =0\)を満たす\(Nx\)は，
\begin{gather}
Nx = \frac{\pi}{2} + k \pi = \frac{(2k+1)\pi}{2} \ \ \
(k = 0, \pm 1, \pm 2, \cdots)
\end{gather}
よって，\(x\) は，
\begin{gather}
x = \pm \frac{(2n+1)\pi}{2N} \ \ \
(n = 0, 1, 2, \cdots, N-1)
\end{gather}
このとき，\(\sin Nx = \pm 1\)．一方，上で示した\(\pm \frac{j}{\varepsilon}\)の虚部より，
\begin{gather}
\pm \frac{1}{\varepsilon} = \sin Nx \sinh Ny
\nonumber \\
\frac{1}{\varepsilon} = \pm \sinh Ny
\end{gather}
よって，\(y\) は，
\begin{gather}
y = \pm \frac{1}{N} \sinh ^{-1} \frac{1}{\varepsilon}
\end{gather}
ここで，\(-js = \cos (x+jy)\)より，零点\(s\)は，
\begin{eqnarray}
s &=& j \cos (x+jy)
\nonumber \\
&=& j (\cos x \cosh y - j \sin x \sinh y)
\nonumber \\
&=& j \cos x \cosh y + \sin x \sinh y
\nonumber \\
&\equiv & \sigma_n + j \omega_n = s_n
\end{eqnarray}
実現可能な回路を得るためには，複素平面の左半面にある零点\(s_n\)を選べばよいので，
\(\Re (s_n) = \sigma_n \lt 0\) ゆえ，
\begin{eqnarray}
\sigma_n &=& - \sin \frac{(2n+1)\pi}{2N} \sinh a
\\
\omega_n &=& \cos \frac{(2n+1)\pi}{2N} \cosh a
\end{eqnarray}
ここで，
\begin{gather}
a = \frac{1}{N} \sinh ^{-1} \frac{1}{\varepsilon}
\end{gather}
伝達関数の零点
\(|H(s)|^2\)は，
\begin{eqnarray}
|H(s)|^2 &=& 1+\varepsilon^2 T_N^2 (-js)
\nonumber \\
&=& 1+\varepsilon^2 \left\{ 2^{N-1} (-js)^N + \cdots \right\}^2
\nonumber \\
&=& \varepsilon^2 2^{2(N-1)} (-1)^N s^{2N} + \cdots
\end{eqnarray}
零点\(s_n\)より伝達関数\(H(s)\)，さらには反射係数\(\Gamma(s)\)は，
\begin{gather}
H(s) = \pm \varepsilon 2^{N-1} (-j)^N \prod _{n=1}^N \left( s-s_n \right)
\\
\Gamma(s) = \frac{K(s)}{H(s)}
= \pm \frac{T_N (\Omega)}{\displaystyle{2^{N-1} (-j)^N \prod _{n=1}^N \left( s-s_n \right)}}
\end{gather}
また，上で求めた\(\sigma_n\)，\(\omega_n\)より，
\begin{gather}
\sin^2 \frac{(2n+1)\pi}{2N} + \cos^2 \frac{(2n+1)\pi}{2N}
= \frac{\sigma_n^2}{\sinh ^2a} + \frac{\omega_n^2}{\cosh ^2a} = 1
\end{gather}
これより，零点\(s_n\)は複素平面のだ円（直交するだ円の軸は実軸と虚軸）上にあることがわかる．
下の図は，\(N=2,3,4,5\)の0.5dB等リップル特性における\(s_n\)を各々，プロットしたもので，\(s_n\)がだ円上にあることが確認できる．
\(s_n\)の位置（\(N=2\)）
\(s_n\)の位置（\(N=3\)）
\(s_n\)の位置（\(N=4\)）
\(s_n\)の位置（\(N=5\)）
周波数特性
\(|H|^2\) dB，Arg\((1/H)\) deg，\(1/|\Gamma|^2\) dBの周波数特性を示すと次のようになり，\(N=2\)から，順次，段数\(N\)を増やした特性を追加してプロットしている．
0.5dBの等リップル特性の低域通過特性（\(N=2\)）
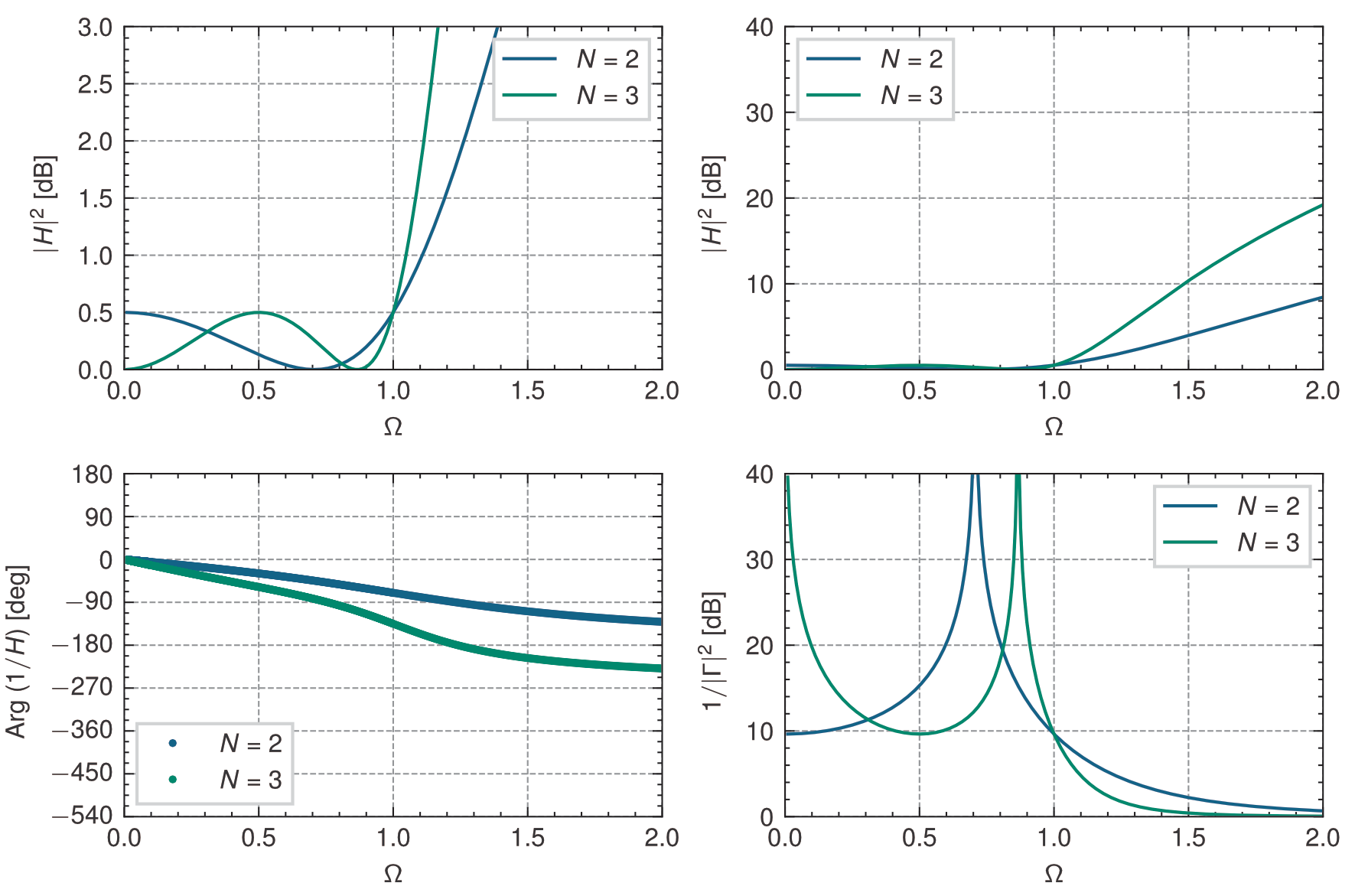0.5dBの等リップル特性の低域通過特性（\(N=2,3\)）
0.5dBの等リップル特性の低域通過特性（\(N=2,3,4\)）
0.5dBの等リップル特性の低域通過特性（\(N=2,3,4,5\)）
リプルを0.05dBとしたときは次のようになり，帯域内はもちろん所定のリプルとなるが，帯域外は上の図（リプル0.5dB）に比べて緩やかな特性に変化していることが確認できる．
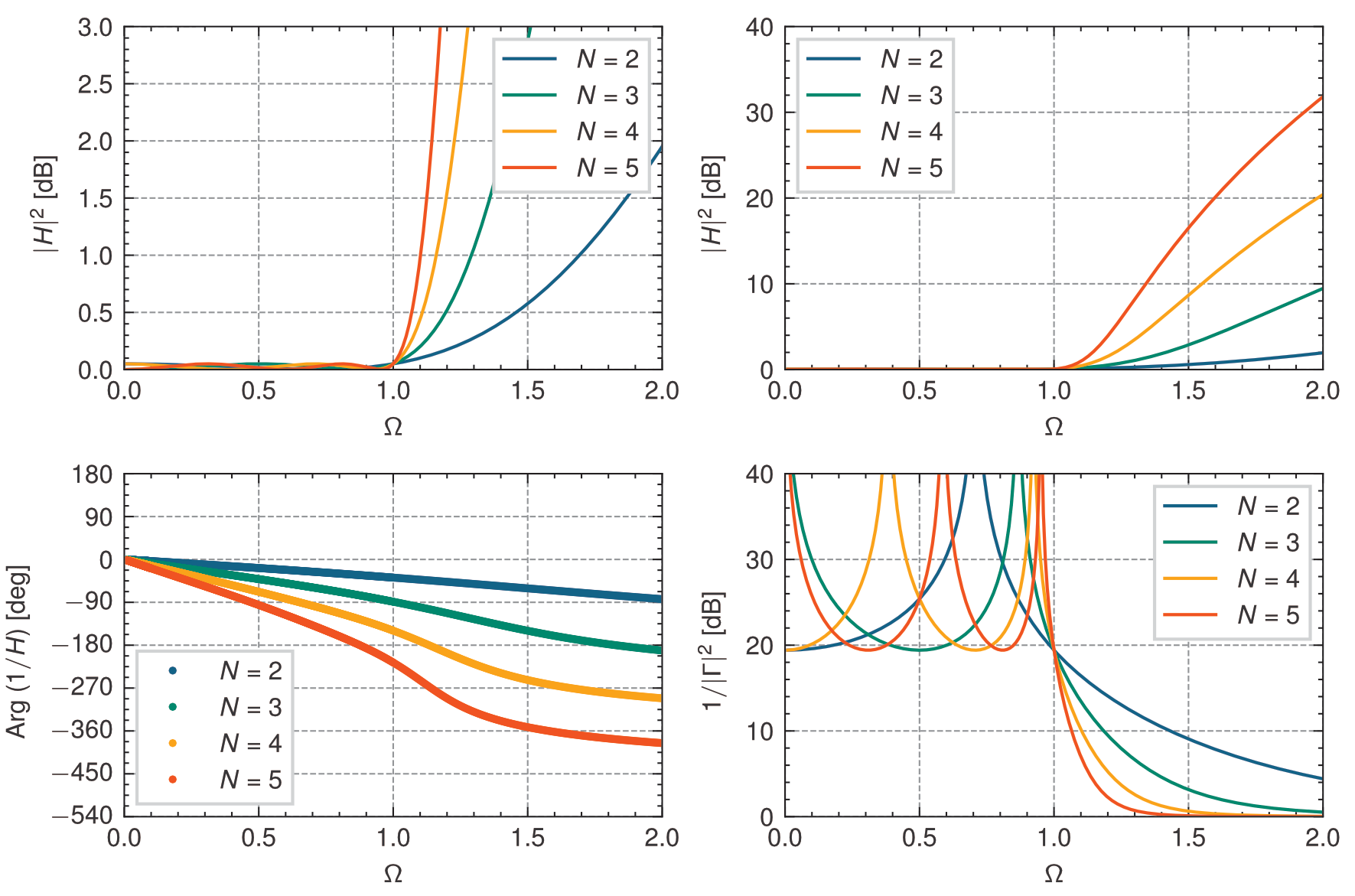0.05dBの等リップル特性の低域通過特性（\(N=2,3,4,5\)）