周波数変換により求めた最平坦特性を持つ帯域阻止梯子型回路の規格化素子値
帯域阻止フィルタは，周波数変換より，
\begin{gather}
s = \frac{1}{\frac{1}{W} \left( \hat{s} + \frac{1}{\hat{s}} \right)}
\end{gather}
これより，直列素子の正規化インピーダンス\(z_k\)は，
\begin{eqnarray}
z_k &=& s g_k
= \frac{g_k}{\frac{1}{W} \left( \hat{s} + \frac{1}{\hat{s}} \right)}
\nonumber \\
&=& \frac{1}{\hat{s} \frac{1}{Wg_k} + \frac{1}{\hat{s} Wg_k}}
\nonumber \\
&\equiv& \frac{1}{\hat{s} \hat{c}_k + \frac{1}{\hat{s} \hat{l}_k}}
= \frac{1}{\hat{y}_k}
\end{eqnarray}
並列接続された規格化キャパシタンス\(\hat{c}_k\)，
規格化インダクタンス\(\hat{l}_k\)は（並列共振回路），
\begin{eqnarray}
\hat{c}_k &=& \frac{1}{Wg_k} \equiv \hat{g}_k
\\
\hat{l}_k &=& Wg_k \equiv \hat{g}'_k
\end{eqnarray}
また，並列素子の正規化アドミタンス\(y_k\)は，
\begin{eqnarray}
y_k &=& s g_k = \frac{g_k}{\frac{1}{W} \left( \hat{s} + \frac{1}{\hat{s}} \right)}
\nonumber \\
&=& \frac{1}{\hat{s} \frac{1}{Wg_k} + \frac{1}{\hat{s} Wg_k}}
\nonumber \\
&\equiv& \frac{1}{\hat{s} \hat{l}_k + \frac{1}{\hat{s} \hat{c}_k}}
= \frac{1}{\hat{z}_k}
\end{eqnarray}
直列接続された規格化キャパシタンス\(\hat{l}_k\)，規格化インダクタンス\(\hat{c}_k\)は（直列共振回路），
\begin{eqnarray}
\hat{l}_k &=& \frac{1}{Wg_k} \equiv \hat{g}_k
\\
\hat{c}_k &=& Wg_k \equiv \hat{g}'_k
\end{eqnarray}
したがって，帯域阻止梯子型回路は双対的な次のような回路で表される．
\(z_{in}^+\)により合成した原型低域通過回路を周波数変換した帯域阻止梯子型回路
\(z_{in}^-\)により合成した原型低域通過回路を周波数変換した帯域阻止梯子型回路
最平坦特性を有する帯域阻止フィルタ（比帯域\(W=0.3\)）の規格化素子値\(\hat{g}_k\)，\(\hat{g}_k'\)を求めると次のようになる．ただし，\(g_0 =1\)，\(g_{N+1}=1\)．
\begin{array}{c|cccccccc}
\hline
N & \hat{g}_1 & \hat{g}_2 & \hat{g}_3 & \hat{g}_4 & \hat{g}_5 & \hat{g}_6 & \hat{g}_7 \\
{} & \hat{g}'_1 & \hat{g}'_2 & \hat{g}'_3 & \hat{g}'_4 & \hat{g}'_5 & \hat{g}'_6 & \hat{g}'_7 \\
\hline \hline
2 & 2.3570 & 2.3570 & & & & \\
{} & 0.4243 & 0.4243 & & & & \\ \hline
3 & 3.3333 & 1.6667 & 3.3333 & & & \\
{} & 0.3000 & 0.6000 & 0.3000 & & & \\ \hline
4 & 4.3552 & 1.8040 & 1.8040 & 4.3552 & & \\
{} & 0.2296 & 0.5543 & 0.5543 & 0.2296 & & \\ \hline
5 & 5.3934 & 2.0601 & 1.6667 & 2.0601 & 5.3934 & \\
{} & 0.1854 & 0.4854 & 0.6000 & 0.4854 & 0.1854 & \\ \hline
6 & 6.4395 & 2.3570 & 1.7255 & 1.7255 & 2.3570 & 6.4395 & \\
{} & 0.1553 & 0.4243 & 0.5796 & 0.5796 & 0.4243 & 0.1553 & \\ \hline
7 & 7.4899 & 2.6731 & 1.8499 & 1.6667 & 1.8499 & 2.6731 & 7.4899\\
{} & 0.1335 & 0.3741 & 0.5406 & 0.6000 & 0.5406 & 0.3741 & 0.1335\\ \hline
\hline
\end{array}
これより，\(N=2,3,4, 5\)について入力インピーダンス\(z_{in}^+\)で合成した回路の特性を求めると次のようになる．
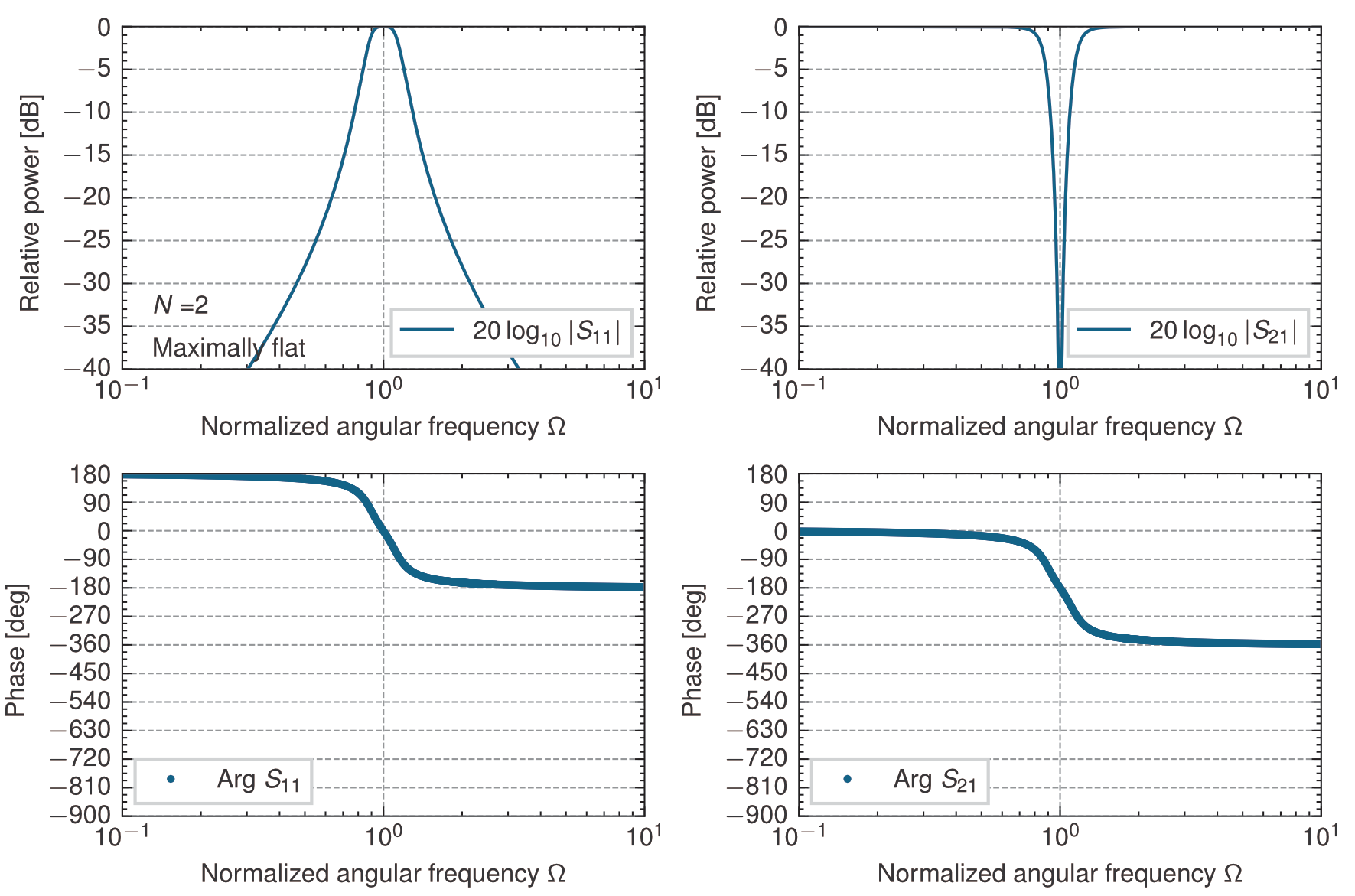2段梯子型回路の帯域阻止特性（\(z_{in}^+\)，\(W=0.3\)）
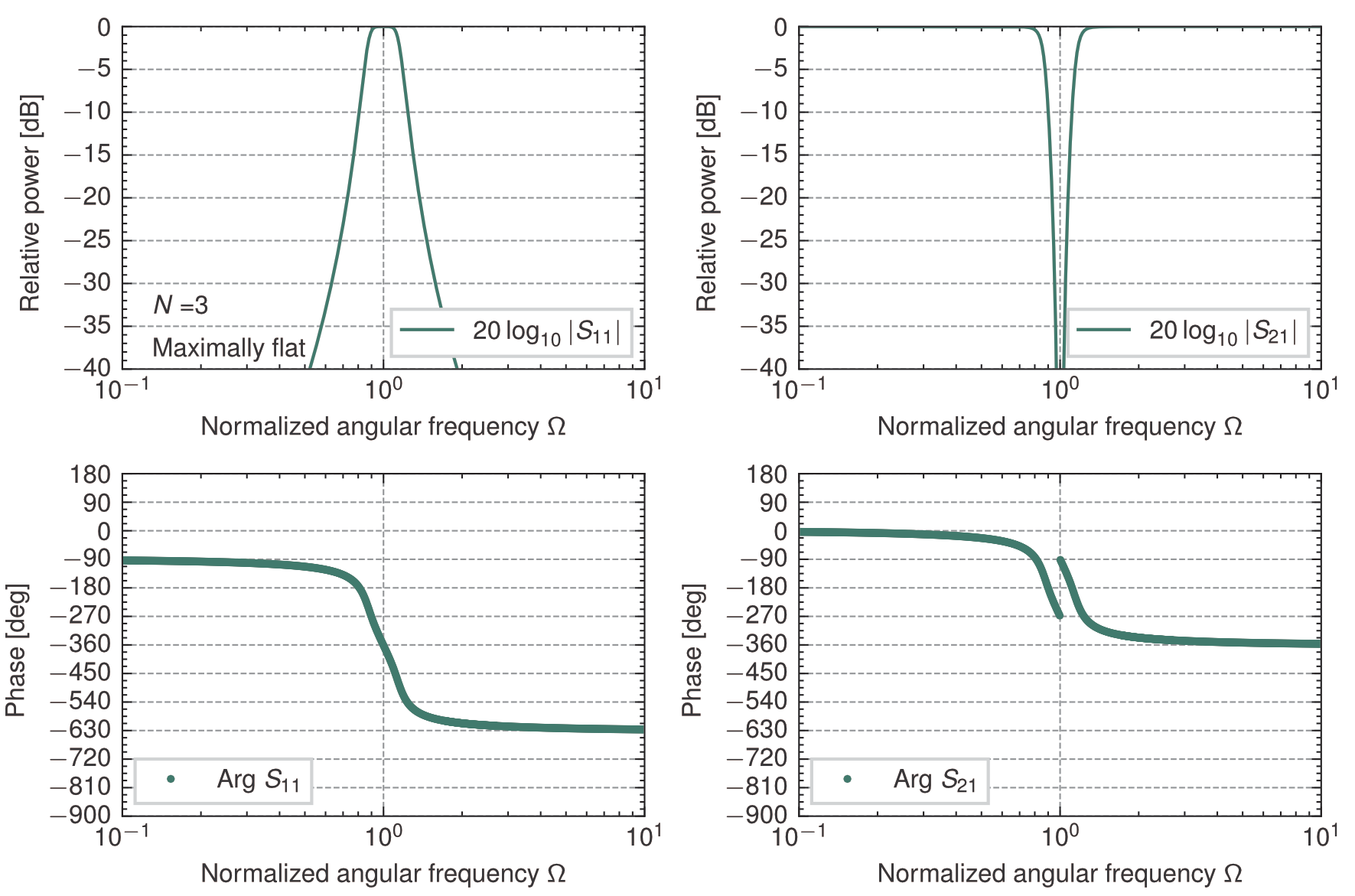3段梯子型回路の帯域阻止特性（\(z_{in}^+\)，\(W=0.3\)）
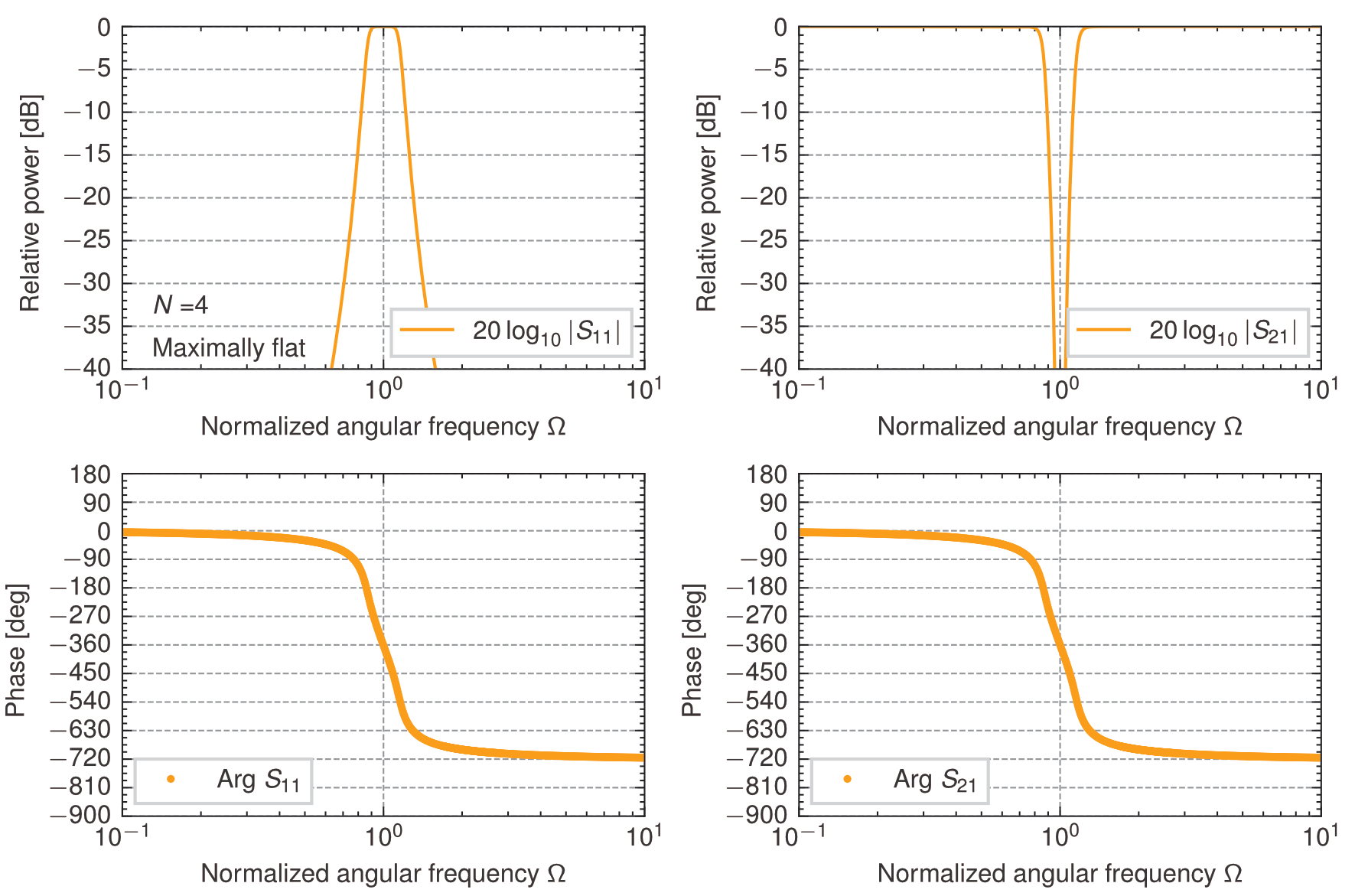4段梯子型回路の帯域阻止特性（\(z_{in}^+\)，\(W=0.3\)）
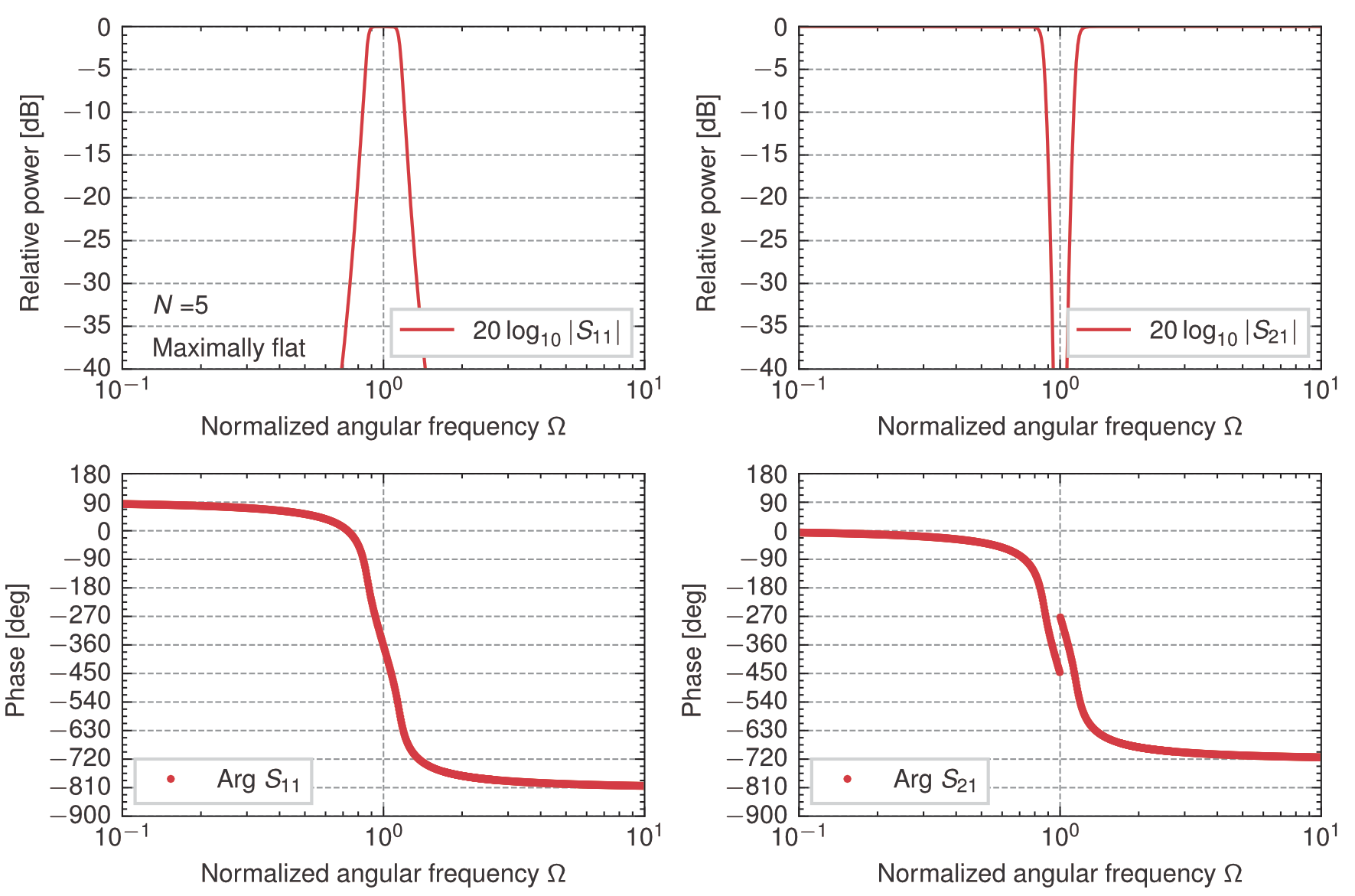5段梯子型回路の帯域阻止特性（\(z_{in}^+\)，\(W=0.3\)）