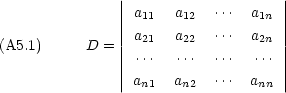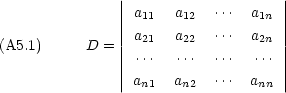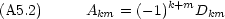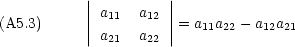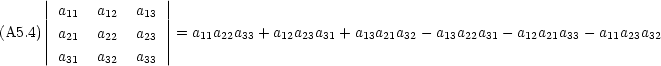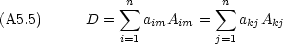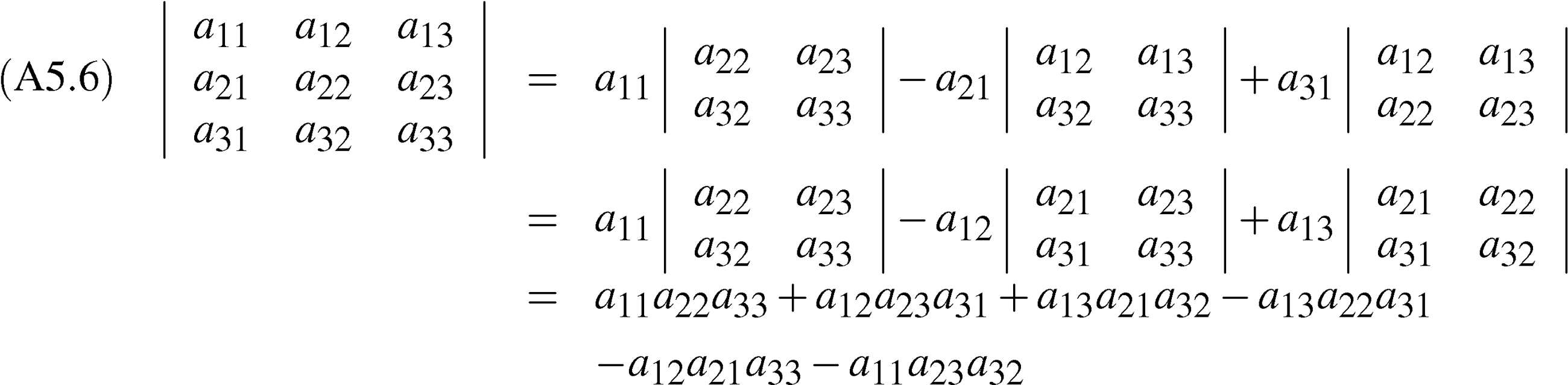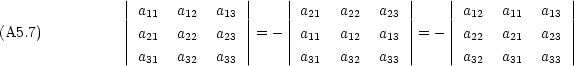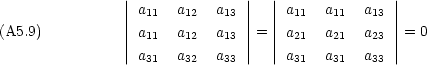A-5 行列式の計算

A-5.1 行列式

行列式はスカラーである

a5-1
aij を要素，横の並び i を行，縦の並び j を列という

行列式 D から k 番目の行と m 番目の列とを取り去った行列式を小行列式 Dkm という

次の式で定義される Akm を余因子という。

a5-2

A-5.2 二次元の場合

a5-3

A-5.3 三次元の場合

俗に言う「たすき掛け」で計算できる。

a5-4
注意： 二次元の行列式の計算法も「たすき掛け」と呼ばれることがあるが，三次元の「たすき掛け」と計算法が異なる。
三次元の方法をそのまま二次元に当てはめると，答えが常にゼロになる。

A-5.4 一般の場合

四次元以上の行列式の計算には簡便な公式はない。

一般的には n 次元の行列式について

a5-5
この式 を用いれば n 次元の行列式を (n- 1) 次元の行列式の線形結合で表すことができるので，最終的に 2 次元の行列式の計算に帰着する。

スカラーそのものを一次元の行列式？と考えれば，二次元の行列式もこの式をみたす。

三次元の行列式も当然この式をみたす。

a5-6

A-5.5 行列式の性質

  1. 行または列を入れかえると符号が変わる
    a5-7
  2. ある行または列の要素をすべて c 倍すると行列式の値が c 倍される
    a5-8
  3. 二つの行または列が等しいとき行列式はゼロになる
    a5-9
  4. ある行を c 倍して他の行に加えても行列式の値は変わらない。列に関しても同様。
    a5-10

演習問題

  1. 行列式の性質 (1)〜(4) を証明せよ。
  2. n 次元の正方行列 A と B の積 A × B の行列式は A 及び B の行列式とどのような関係にあるか。