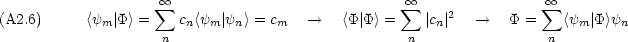n = An
n = An n,
n,  n : 固有関数, An : 固有値
n : 固有関数, An : 固有値
演算子Â の固有値方程式 Â n = An
n = An n,
n,  n : 固有関数, An : 固有値
n : 固有関数, An : 固有値
任意の複素関数 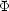 と
と  について<
について< |
|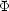 >* = <
>* = <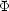 |
| >
>
次の条件を満たす時, 2 つの演算子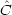 ,
, ![]() + はエルミート共役であるという
+ はエルミート共役であるという
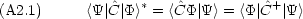
特に,自分自身とエルミート共役である演算子をエルミート演算子という
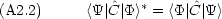
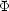 =
=  =
=  がエルミート演算子
がエルミート演算子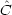 の固有関数, C を対応する固有値とする
の固有関数, C を対応する固有値とする
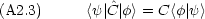
 |
|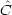 |
| >* = <
>* = < |
|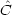 |
| >
>エルミート演算子の異なる固有値に属する固有関数は直交する。
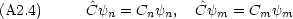
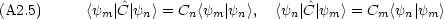
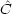 はエルミート演算子だから<
はエルミート演算子だから< m|
m|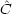 |
| n> = <
n> = < n|
n|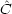 |
| m>すなわち Cn<
m>すなわち Cn< m|
m| n> = Cm<
n> = Cm< n|
n| m>
m>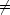 0, Cm
0, Cm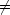 0, Cn
0, Cn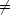 Cm だから <
Cm だから < m|
m| n> = <
n> = < n|
n| m> = 0
m> = 0
任意の複素関数について 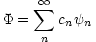
係数 cn を求めるには,左から  m* を掛けて全空間で積分する
m* を掛けて全空間で積分する