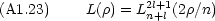dinger 方程式の動径部分
dinger 方程式の動径部分
水素原子に対する Schr dinger 方程式の動径部分
dinger 方程式の動径部分
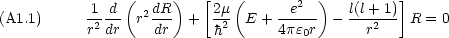
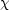 (r) = rR(r) と置いて次の変数変換を行う。(N は規格化定数)
(r) = rR(r) と置いて次の変数変換を行う。(N は規格化定数)

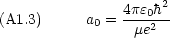

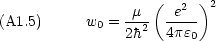
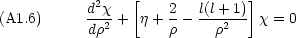
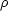 が無限大の時の漸近解
が無限大の時の漸近解
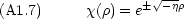
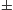 のうち - の方)だけが物理的に意味がある。
のうち - の方)だけが物理的に意味がある。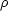 について,次の仮定を置く
について,次の仮定を置く
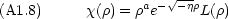
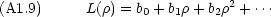
 を求めることにする。さて
を求めることにする。さて
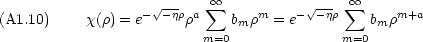
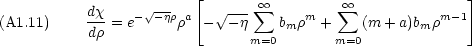
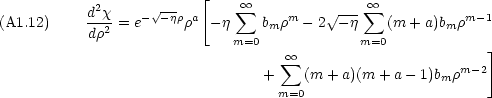
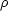 2 をかけ, e-
2 をかけ, e-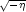

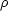 a でくくると次のようになる
a でくくると次のようになる
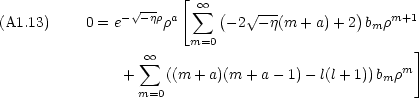
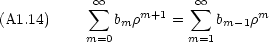
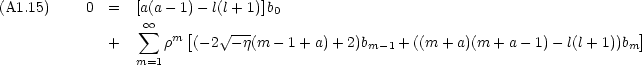
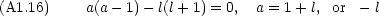
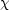 が
が 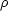 = 0 で発散することになるので, a > 0 でなければならないから
= 0 で発散することになるので, a > 0 でなければならないから

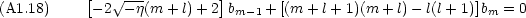
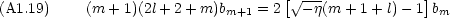
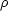 ) が解った。ただし,この無限級数は発散するので,発散しないように nr 項目までの有限級数(多項式)になるようにする。
) が解った。ただし,この無限級数は発散するので,発散しないように nr 項目までの有限級数(多項式)になるようにする。
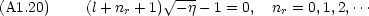
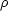 ) は nr 次の多項式になる。また
) は nr 次の多項式になる。また
ところで,次の式で与えられる多項式を Laguerre の陪多項式という。
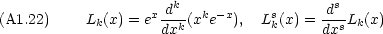
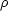 ) との関係は
) との関係は