 電子系に対する Hückel 法がある。
電子系に対する Hückel 法がある。共役
 電子系とは,一重結合と二重結合が交互に現れるような系である。(副読本 pp. 142〜162)
電子系とは,一重結合と二重結合が交互に現れるような系である。(副読本 pp. 142〜162)
分子軌道法の簡単かつきわめて有用な応用に,共役  電子系に対する Hückel 法がある。
電子系に対する Hückel 法がある。
共役  電子系とは,一重結合と二重結合が交互に現れるような系である。(副読本 pp. 142〜162)
電子系とは,一重結合と二重結合が交互に現れるような系である。(副読本 pp. 142〜162)
LCAO 分子軌道 
エネルギー期待値
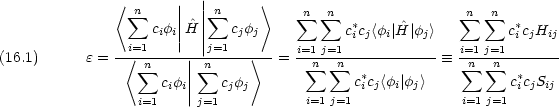

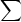 i=1n
i=1n 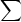 j=1nci*cjSij =
j=1nci*cjSij = 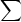 i=1n
i=1n 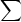 j=1nci*cjHij
j=1nci*cjHij が最小になる ci の組を求める
が最小になる ci の組を求める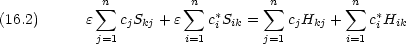
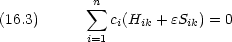
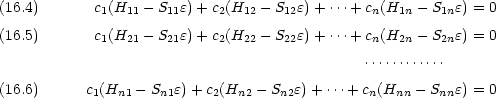
 が必要 → 永年方程式
が必要 → 永年方程式
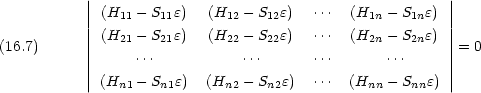
 が求められたら,先の連立方程式と規格化条件とから ci を求める
が求められたら,先の連立方程式と規格化条件とから ci を求める
共役二重結合系の炭素鎖を対象とする。よって,骨格を構成する要素は全て同種原子である。
仮定として,  結合と
結合と  結合とを全く独立に取り扱う。その中で,
結合とを全く独立に取り扱う。その中で,  電子系のみに着目する。つまり,原子軌道として p 軌道のみを考慮する。
電子系のみに着目する。つまり,原子軌道として p 軌道のみを考慮する。
Hii =  とおく(全ての i で同じ値)
とおく(全ての i で同じ値)
Sii = 1 である(規格化条件)
近似その 1 i 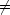 j のとき Sij = 0
j のとき Sij = 0
近似その 2 i  j のときで i と j との間に結合が j のときで i と j との間に結合が
|
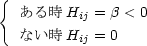
|
n 個の原子軌道から n 個の MO が出来る。
基底状態では,エネルギーの低い MO から順に 2 個づつの  電子が占有。
電子が占有。
電子間反撥を無視した場合の全  電子エネルギー E
電子エネルギー E
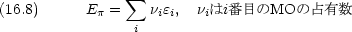
 電子密度 qr
電子密度 qr
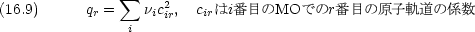
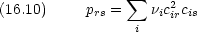
sp2 混成軌道は C-C の  結合と C-H 結合に使われ, p 軌道は
結合と C-H 結合に使われ, p 軌道は  結合に使われる。炭素 1 と 2 の p 軌道の波動関数を
結合に使われる。炭素 1 と 2 の p 軌道の波動関数を 1,
1,  2 とする
2 とする
分子軌道
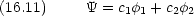
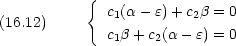
永年方程式
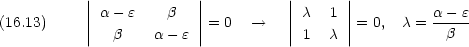
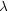 2 - 1 = 0
2 - 1 = 0 
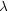 =
= 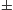 1 から直ちにエネルギー準位が判る
1 から直ちにエネルギー準位が判る 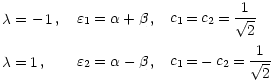
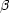 < 0 であるから,
< 0 であるから, 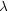 = -1 の方が基底状態である。
= -1 の方が基底状態である。
 電子は 2 個なので,基底状態の MO に二つの電子が入る
電子は 2 個なので,基底状態の MO に二つの電子が入る
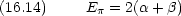
MO 法による水素分子と酷似している。
|
永年方程式
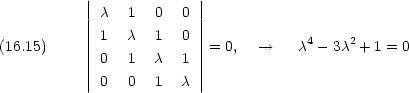
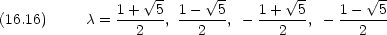
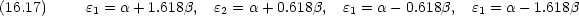
 電子は 4 個有るので,一番下と下から 2 番目の準位に二つづつの電子が入る
電子は 4 個有るので,一番下と下から 2 番目の準位に二つづつの電子が入る
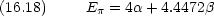
 電子エネルギーはエチレン 2 個分の 4(
電子エネルギーはエチレン 2 個分の 4( +
+ 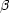 )
)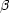
|
演習問題
 電子系に対する単純 Hückel 法とはどのような近似法か説明せよ。
電子系に対する単純 Hückel 法とはどのような近似法か説明せよ。
 電子について,単純 Hückel 法を用いて考察する。
電子について,単純 Hückel 法を用いて考察する。
 電子エネルギーを求めよ。
電子エネルギーを求めよ。
 電子について,単純 Hückel 法を用いて考察する。
電子について,単純 Hückel 法を用いて考察する。
 電子エネルギーを求めよ。
電子エネルギーを求めよ。
 電子密度を求めよ。
電子密度を求めよ。
 電子について,単純 Hückel 法を用いて次の関数及び量を求めよ。
電子について,単純 Hückel 法を用いて次の関数及び量を求めよ。  電子エネルギー。非局在化エネルギー。各炭素原子の
電子エネルギー。非局在化エネルギー。各炭素原子の  電子密度。各結合の次数。
電子密度。各結合の次数。
 電子エネルギー。非局在化エネルギー。各炭素原子の
電子エネルギー。非局在化エネルギー。各炭素原子の  電子密度。各結合の次数。
電子密度。各結合の次数。
 電子について,単純 Hückel 法を用いて次の関数及び量を求めよ。
電子について,単純 Hückel 法を用いて次の関数及び量を求めよ。 電子エネルギー。非局在化エネルギー。各炭素原子の
電子エネルギー。非局在化エネルギー。各炭素原子の  電子密度。各結合の次数。
電子密度。各結合の次数。