15 混成軌道

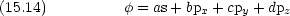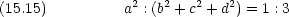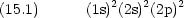
原子価結合法を多原子分子に適用したとき，原子軌道をそのままの形で考えていたのでは分子の構造を正しく説明出来ないことがある。
そのときに，混成軌道という考え方を用いればうまく説明できることがある。

15.1 メタンの構造

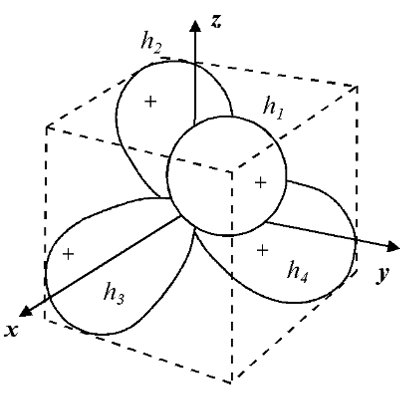
CH₄ の 4 つの水素は化学的に等価であることが知られている。つまり，炭素の 4 つの結合は等価でなければならない。
しかし，炭素原子の電子構造は

であり，炭素は 2 価であると考えられる。この矛盾を説明するために昇位ということを考える

昇位に必要なエネルギーは結合で補填されると考えられるが，その際，軌道の混成が生じると考える。

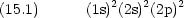
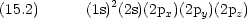
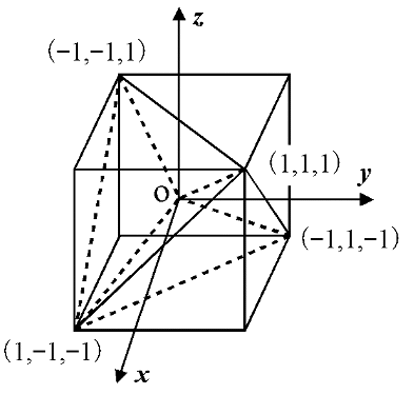
原点に C を置いたときの H の座標は (1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1) なので

規格化条件・直交条件

よって

このような軌道を sp³ 混成軌道 hybrid orbital という

15.2 エチレン

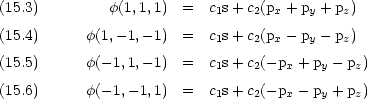
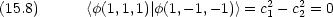
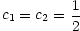
平面構造
z 軸を分子面に垂直な軸とする
s, p_x, p_y のあいだで混成が起こる
（xy 面は pz 軌道の節面である）

このような軌道を sp² 混成軌道という

15.3 アセチレン

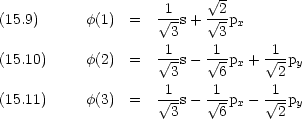
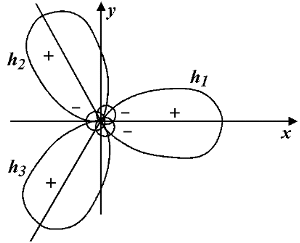
直線型構造
x 軸を分子軸とする
s, p_x のあいだで混成が起こる

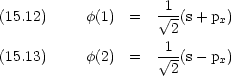
-1-(15.12) f(1) = V~ 2(s+ px) 1(15.13) f(2) = V~ 2(s- px)

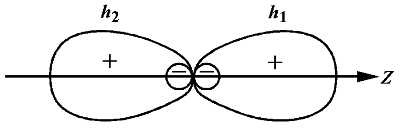
このような軌道を sp 混成軌道という

15.4 σ結合・π 結合

　

結合軸を含む共通な節面を fig

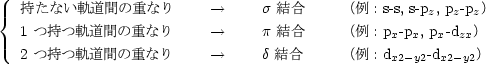
2 重結合等を考える場合に重要

15.5 その他の混成軌道

混成軌道	軌道数	立体構造	結合角	例
dsp²	4	正方形	90^o	Ni(CN)₄^2-, AuCl₄^-
sp³d	5	三方両錐	90^o, 120^o, 180^o	PCl₅, AsF₅, SbCl₅
d²sp³	6	正八面体	90^o	Co(NH₃)₆³⁺, PtCl₆^2-
sp³d²	6	正八面体	90^o	SF₆

演習問題

メタンの 4 つの結合は等価で，原点に C を置いたときの H の座標は (1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1) である。
1. 炭素の 2s, 2p_x, 2p_y, 2p_z の 4 つの軌道の線形結合によって，それぞれの結合に関与している混成軌道を表せ。規格化すること。
2. (1) で求めたの 4 つの軌道は互いに直交していることを示せ。
3. (1) で求めたの 4 つの軌道で， 2s の係数の 2 乗と， 2p の 3 つの軌道の係数の 2 乗を足しあわせたものとの比は 1:3 であることを示せ。
炭素の sp³ 混成軌道は一般に次のような形に書ける。

そして，次の関係が知られている。
1. 混成軌道のうち 1 つの軌道が x 軸の方向を向いているとする。規格化された波動関数の a, b, c, d を求めよ。
2. 次の混成軌道は xz 面内に中心線があるとする。この軌道の波動関数が (1) の波動関数と直交していることを利用して，規格化された波動関数の a, b, c, d を求めよ。
3. 波動関数が最大になる方向を軌道の方向とする。 (1), (2) の波動関数を角度について微分し， 2 つの軌道のなす角を求めよ。
4. 第 3, 第 4 の混成軌道の波動関数は (1), (2) の波動関数のどちらとも直交しており， xz 面について対称である。
  規格化された波動関数の a, b, c, d を求めよ。
炭素の sp² 混成軌道が xy 面内にあるとする。
1. 混成軌道の波動関数は，炭素の 2s, 2p_x, 2p_y, 2p_z の 4 つの軌道の波動関数を用いると一般にどのような形に書けるか。
2. 3 つの混成軌道の規格化された波動関数を書け。
3. (2) で求めた 3 つの混成軌道の波動関数が互いに直交していることを示せ。
4. (2) で求めた 3 つの混成軌道なす角を求めよ。
アセチレンは直線型分子である。結合に関与している炭素の混成軌道について説明せよ。
次のような混成軌道を持つと考えられる分子の例をあげ，分子構造について述べよ。
1. dsp²
2. sp³d
3. d²sp³
4. sp³d²