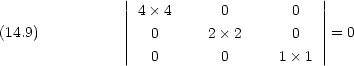|
酸素原子 (1s)2 (2s)2 (2px)2 (2py)(2pz) 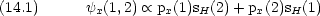
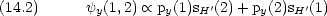
|
|
原子価結合法,分子軌道法を一般の多原子分子に適用する方法について述べる。
|
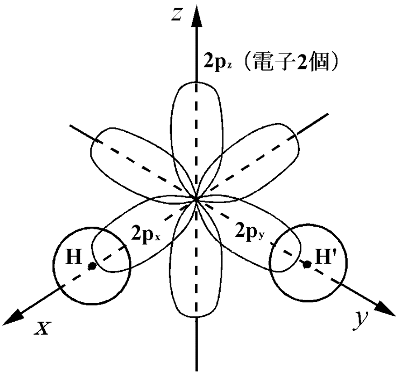
酸素原子 (1s)2 (2s)2 (2px)2 (2py)(2pz) 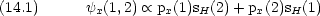
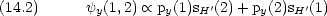
|

|
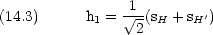
|
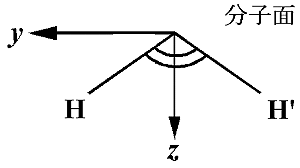
|
|
軌道の対称性
|
|
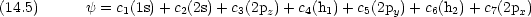
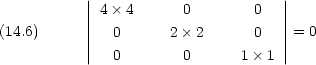
複雑な分子については群論の助けをかりると簡単化できる場合がある。
核の配置を変えてエネルギーの低いところを探すので分子構造の予測がしにくいという欠点があるが, VB 法に比べて計算が単純である。
|
|
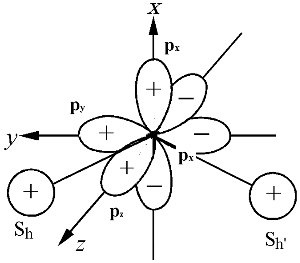
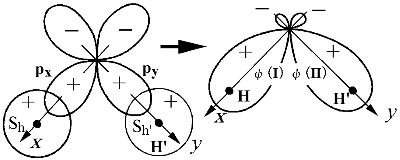
VB 法的考え方を MO に取り込む 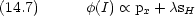
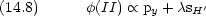
|
|
 (I),
(I),  (II) と対称性が違う
(II) と対称性が違う  (I) と
(I) と  (II) とは重なりがほとんどない
(II) とは重なりがほとんどない (I),
(I),  (II), pz は独立
(II), pz は独立