13 二原子分子
水素分子の場合,結合を作る原子が同種だったので対称性から様々なことが直観的に分かる。
一般の二原子分子の場合も,それぞれの軌道の対称性を考えると,生じる結合についてある程度の性質を予想することが出来る。
13.1 一般的原則
AO の重なり積分がゼロ → 共鳴積分がゼロ → 分子軌道を作らない
HAA ≫ HBB  cA
cA 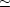 1, cB
1, cB 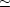 0
0  分子軌道を作らない
分子軌道を作らない
s-pz 相互作用の大きさが問題
13.2 等核二原子分子
| 分子 |
電子の配置 |
結合の多重度(次数) |
|
|
 s s |
|
 s* s* |
|
 p p |
|
 p p |
|
 p* p* |
|
 p* p* |
| 2 |
|
|
|
|
|
|
|
|
|
|
| 2 |
|
2 |
|
|
|
|
|
|
|
|
| 2 |
|
2 |
|
2 |
|
4 |
|
|
|
|
| 2 |
|
2 |
|
2 |
|
4 |
|
2 |
|
|
|
|
13.3 異核二原子分子
非結合性軌道
孤立電子対
13.4 双極子モーメント
分子の中の電気的な偏りを表す量の一つに双極子モーメントがある。分子軌道法による双極子モーメントの計算法を述べる。
zAA はA の核の位置に, zBB は B の核の位置に一致するはずである。つまり
核間距離を R として
zAB 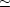 0 として,
0 として,  に 2 つの電子が入っているとすると
に 2 つの電子が入っているとすると
演習問題
- 2 つの原子 A, B がある。
- それぞれの原子軌道
 A,
A,  B の線形結合を MO に用いた変分法から,次の永年方程式が導かれることを示せ。
ただし
B の線形結合を MO に用いた変分法から,次の永年方程式が導かれることを示せ。
ただし
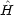 eff はその MO 中の電子に対する有効 1 電子ハミルトニアンである。
eff はその MO 中の電子に対する有効 1 電子ハミルトニアンである。
- 永年方程式を解いてエネルギーを計算せよ。
 A =
A =  B =
B =  である時 (2) の答えはどのようになるか。
である時 (2) の答えはどのようになるか。
 A ≫
A ≫ B のとき (2) の答えは次のようになることを示せ。
B のとき (2) の答えは次のようになることを示せ。
- (4) の結果から
 A と
A と  B の差が非常に大きいとき
B の差が非常に大きいとき  A と
A と  B とは分子軌道を作りにくい事について論じよ。
B とは分子軌道を作りにくい事について論じよ。
- 2 つの原子 A, B の原子軌道について,重なり積分がゼロになるような組み合わせの例を挙げよ。
- 分子の電子配置に対する構成原理とはどのような原理か。
 結合,
結合,  結合,
結合, 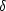 結合とはそれぞれどのような結合を表すか。
結合とはそれぞれどのような結合を表すか。
- 2 原子分子の分子軌道について,次の記号で表される軌道はどのような軌道か。
 1s
1s
 *1s
*1s
 2pz
2pz
 2p
2p
- 2 原子分子の結合について分子軌道法的に考察する。
- 結合次数はどのように定義されるか。
- H2, H2+, H2- の結合次数を求めよ。これらの分子は安定に存在すると考えられるか。
- He2, He2+ の結合次数を求めよ。これらの分子は安定に存在すると考えられるか。
- 等核 2 原子分子を分子軌道法的に考察する。
- B2 の基底状態は三重項状態で常磁性を示す。これからどのようなことが解るか。
- N2 と N2+ はどちらが解離エネルギーが大きいか予測せよ。実験的には前者が大きい。
- O2 と O2+ はどちらが解離エネルギーが大きいか予測せよ。実験的には後者が大きい。
- O2+, O2, O2-, O22- の結合長と結合エネルギーについて知りうるところを述べよ。
- NO と NO+ の基底状態電子配置と結合次数を書け。
- シアン化物イオンの結合次数を書け。
- 分子内の原子間ポテンシャルの極小から計算した解離エネルギーを平衡解離エネルギー De という。それに対して,基底状態から計算した解離エネルギーをしばしば分光学的解離エネルギー D0 と呼 ぶ。
- De と D0 の差は何か。
- N2 の平衡解離エネルギーは 9.902 eV, 基準振動数は 2331 cm-1 である。分光学的解離エネルギーを見積もれ。
- H2 について (2) と同様の計算を行え。ただし, De = 4.748 eV, 基準振動数は 4401 cm-1 である。
- NaCl の平衡核間距離は 0.2361 nm, 気体の NaCl が原子に解離する平衡解離エネルギーは 4.29 eV である。また, Na のイオン化エネルギーは 5.14 eV, Cl の電子親和力は 3.61 eV である。
- NaCl がイオンへ解離するエネルギーを見積もれ。
- NaCl を Na+ イオンと Cl- イオンが Coulomb 力のみで結びついた分子とみなしたとき, NaCl がイオンへ解離するエネルギーを見積もれ。
- (2) と同様の仮定に基づいて NaCl の双極子モーメントを見積もれ。実測値は 3.003 × 10-29 C m である。
- (1)〜(2) の結果を比較してどのようなことがいえるか。
- KF の平衡核間距離は 0.2170 nm, 気体の KF が原子に解離する平衡解離エネルギーは 5.18 eV である。また, Kのイオン化エネルギーは 4.34 eV, F の電子親和力は 3.40 eV である。
- KF がイオンへ解離するエネルギーを見積もれ。
- KF を K+ イオンと F- イオンが Coulomb 力のみで結びついた分子とみなしたとき, KF がイオンへ解離するエネルギーを見積もれ。
- (2) と同様の仮定に基づいて KF の双極子モーメントを見積もれ。実測値は 2.87 × 10-29 C m で ある。
- 2 原子分子の結合性 MO の波動関数が次のように表されるとする。
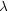 と重なり積分 S から分子の双極子モーメントを見積もる式を導け。
と重なり積分 S から分子の双極子モーメントを見積もる式を導け。
-
次に示す分子の双極子モーメントから
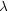
を見積もれ。
また,どちらの原子が +
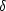
でどちらが-
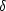
か電気陰性度から予測せよ。ただし,重なり積分はすべて 1/3 であると仮定する。
| 分子 |
HF |
HCl |
HBr |
KI |
KCl |
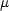 /eR /eR |
0.43 |
0.17 |
0.11 |
0.05 |
0.47 |
 cA
cA 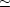 1, cB
1, cB 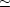 0
0  分子軌道を作らない
分子軌道を作らない cA
cA 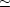 1, cB
1, cB 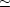 0
0  分子軌道を作らない
分子軌道を作らない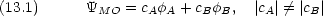
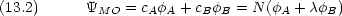
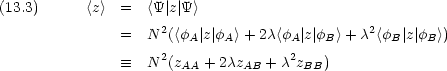
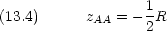
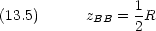
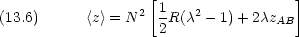
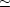 0 として,
0 として,  に 2 つの電子が入っているとすると
に 2 つの電子が入っているとすると
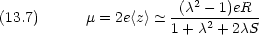
 A,
A,  B の線形結合を MO に用いた変分法から,次の永年方程式が導かれることを示せ。
B の線形結合を MO に用いた変分法から,次の永年方程式が導かれることを示せ。
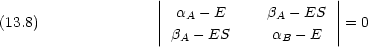
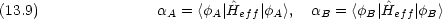

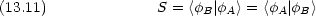
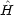 eff はその MO 中の電子に対する有効 1 電子ハミルトニアンである。
eff はその MO 中の電子に対する有効 1 電子ハミルトニアンである。
 A =
A =  B =
B =  である時 (2) の答えはどのようになるか。
である時 (2) の答えはどのようになるか。
 A ≫
A ≫ B のとき (2) の答えは次のようになることを示せ。
B のとき (2) の答えは次のようになることを示せ。
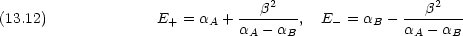
 A と
A と  B の差が非常に大きいとき
B の差が非常に大きいとき  A と
A と  B とは分子軌道を作りにくい事について論じよ。
B とは分子軌道を作りにくい事について論じよ。
 結合,
結合,  結合,
結合, 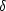 結合とはそれぞれどのような結合を表すか。
結合とはそれぞれどのような結合を表すか。
 1s
1s
 *1s
*1s
 2pz
2pz
 2p
2p
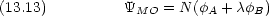
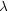 と重なり積分 S から分子の双極子モーメントを見積もる式を導け。
と重なり積分 S から分子の双極子モーメントを見積もる式を導け。
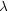 を見積もれ。
を見積もれ。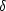 でどちらが-
でどちらが-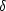 か電気陰性度から予測せよ。ただし,重なり積分はすべて 1/3 であると仮定する。
か電気陰性度から予測せよ。ただし,重なり積分はすべて 1/3 であると仮定する。 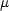 /eR
/eR