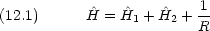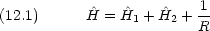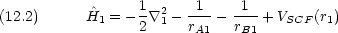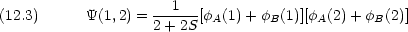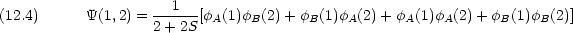12 水素分子〜その 2〜分子軌道法

前の節で用いた分子軌道法を水素分子に応用する。
一電子近似の分子軌道法では，一つの電子が入りうる分子軌道を計算し，そこにエネルギーの低い順に 2 つづつの電子をうめていく。
SCF 的に一電子の感じる有効ポテンシャルを考える必要があるが，最も簡単な近似としては，電子間の反発を全て無視することが考えられる。
（副読本 pp. 134 〜 141）

12.1 水素分子のSCF 近似ハミルトニアン（ 1 電子近似）

12-1
12-2
第 0 次近似としては SCF ポテンシャルがゼロ（あまりよい近似ではない）

12.2 分子軌道法

電子間相互作用を無視した場合，一電子の波動関数は水素分子イオンの場合と全く同じである。
よってそこに 2 つの電子が入ると

12-3
この関数は電子のラベル交換について対称なので，スピン関数は必ず反対称でなければならない。

12.3 原子価結合法との比較

計算結果 平衡核間距離 結合エネルギー
VB 0.086 nm 3.14 eV
MO 0.085 nm 2.68 eV
実験値 0.074 nm 4.74 eV

MO の波動関数（軌道部分）を展開すると次のようになる

12-4
2 つの電子が一方の核に属するのはイオン結合的であり，ひとつの核に 1 つづつの電子が属するのは共有結合的である。
この式を見てわかるように，電子間相互作用を無視した分子軌道法では，共有結合とイオン結合の寄与が 1:1 であ る。

12.4 分子軌道法の改良

Configuration Interaction 異なる電子配置の一次結合で波動関数を作り，変分法を適用
基底関数の問題

演習問題

  1. 水素分子について。
    1. SCF 近似ハミルトニアンとは一般にどのようなものか。
    2. 水素分子に対する SCF 近似ハミルトニアンはどのような形に書けるか。計算不可能な部分は文字のまま残してよい。
  2. 電子間の反撥を無視した場合 LCAO-MO 法による水素分子の基底状態について。
    1. どのような軌道か。関数形を書け。
    2. 電子はどのように軌道を占有するか。
    3. 系全体の波動関数とエネルギーとを求めよ。
    4. スピン波動関数はどのようになるか。
  3. 電子間の反撥を無視した場合 LCAO-MO 法による水素分子の第 1 励起状態について。
    1. 電子はどのように軌道を占有するか。
    2. 波動関数とエネルギーとを求めよ。
  4. 電子間の反撥を無視した場合 LCAO-MO 法による水素分子の基底状態について。
    1. エネルギー準位及び各種積分の表式から，エネルギーの核間距離依存性を図示せよ。
    2. 結合エネルギーを求めよ。
    3. 基準振動数を cm-1 で予測せよ。
  5. 電子間の反撥を無視した場合 LCAO-MO 法による水素分子の基底状態について，イオン結合の寄与と共有結合の寄与の割合はどの程度か。
  6. Configuration Interaction とは何か述べよ。