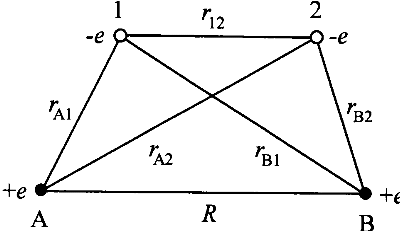
2 つのプロトン A, B 2 つの電子 1, 2 原子核は固定して,電子の運動のみを取り扱う (Born-Oppenheimer 近似) 様々な原子核間距離についてエネルギーを計算し, もっとも安定な配置を求める。 |
|
化学結合を量子力学的に表現するためには大きく分けて,原子価結合法と分子軌道法の二つの方法がある。
原子価結合法は,はじめに独立した原子を考え,結合を作る原子からそれぞれ一つずつの電子が対になって化学結合が生じると考える。共有結合の概念をモデル化したのもであるといえる。歴史的には,Heitler と London によって水素原子に用いられたのが最初である。
2 つのプロトン A, B 2 つの電子 1, 2 原子核は固定して,電子の運動のみを取り扱う (Born-Oppenheimer 近似) 様々な原子核間距離についてエネルギーを計算し, もっとも安定な配置を求める。 |

|
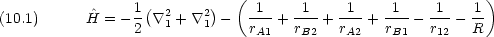
A 原子のみに対するハミルトニアン(原子単位)
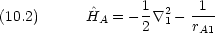
| A 原子の波動関数 |  A(1) A(1) |
B 原子の波動関数 |  B(2) B(2) |
| A 原子のエネルギー | EH = -1/2 (au) | B 原子のエネルギー | -1/2 |
水素分子に対するハミルトニアンは次のように書ける
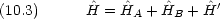
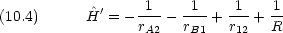
2 つの原子が全く別々に存在している場合,電子 1 は原子 A のみに属し,電子 2 は原子 B のみに属している。
よって,全系の波動関数とエネルギーは次のように書ける。
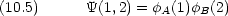
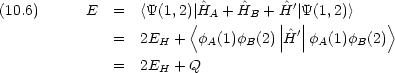
| エネルギーの極小を与える R の値 | 0.09 nm |
| エネルギーの極小値 | 0.25 eV |
二つの原子が近づいて化学結合を形成したとき,電子 1 は原子 A のみに属しているとはいえず,原子 B に属しているとも考えられる。しかも電子 1 と電子 2 は区別できない。よって,全系の波動関数は次のように書けると考えなければ ならない。
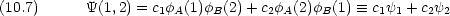
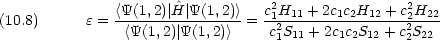
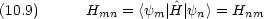
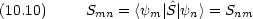
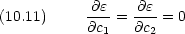
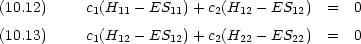
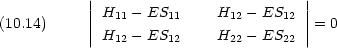

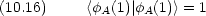
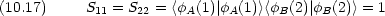
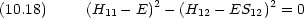
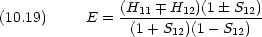
次に波動関数を求める。式 (10.12) を変形すると,次のように書ける
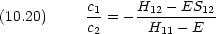
式 (10.20) に式 (10.19) を代入すると,復号の上をとった場合 c1/c2 = -1,下をとった場合 c1/c2 = 1 となる。
よって,答えを次のようにまとめることができる。
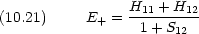
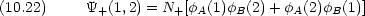
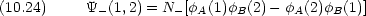
二つの答えのうち  + が低いエネルギーを与える エネルギー -3.14 eV 核間距離 0.087 nm
+ が低いエネルギーを与える エネルギー -3.14 eV 核間距離 0.087 nm
普通つぎのような記号を用いる
重なり積分
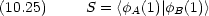
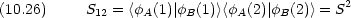
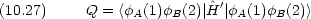
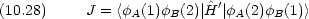
|
今までの計算は,原子軌道をそのまま用いていたが,電子は二つの中心から引力を受けるので,軌道の大きさが原子の場合と異なるはずである。
この効果を取り入れるために,次のような原子軌道関数を考える。
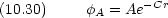
一方の原子の効果で他方の軌道は非対称になるはずである。
つまり,原子軌道は球対称ではない。これを考慮するための原子軌道関数は
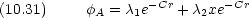
最も簡単な原子価結合法では,原子が互いに電子を交換して電子対を形成すると考えているので,完全に共有結合的である。
一方,イオン結合を考えれば,電子対は両方ともどちらかの原子に属しているはずである。現実は完全な共有結合と完全なイオン結合の中間にあると考えられる。
共有結合
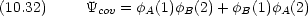
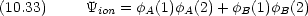
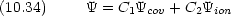
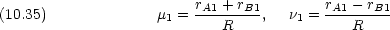
 1 は R を回転軸とし xz 面を基準とした三角形 (A, B, 1) の面の回転角である。
1 は R を回転軸とし xz 面を基準とした三角形 (A, B, 1) の面の回転角である。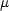 1,
1,  1,
1,  1 で表し,積分の体積素片が次式になることを示せ。
1 で表し,積分の体積素片が次式になることを示せ。
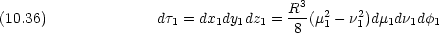
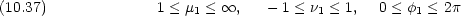
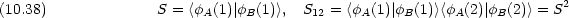
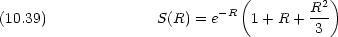
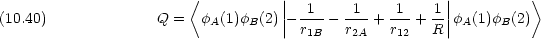
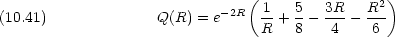
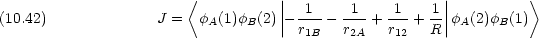
 (1,2) とエネルギー準位を求めよ。
(1,2) とエネルギー準位を求めよ。
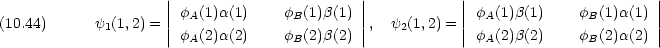
 A は A 原子,
A は A 原子,  B は B 原子の 1s 軌道波動関数である。
B は B 原子の 1s 軌道波動関数である。