電子の場合と異なり, I は整数または半整数(つまり 0, 1/2, 1, 3/2,
 )の値を取りうる。この値は核種によって決まる。
)の値を取りうる。この値は核種によって決まる。
電子だけではなく,陽子や中性子もスピンを持っている。その結果,原子核はそれぞれ固有の核スピンを持っている。
磁場とスピンの相互作用を利用して, NMR のシグナルが観測できる。 NMR は現在の化学にはなくてはならない実験手段であり,物理化学だけではなく有機化学の分野でも広く用いられている。
(副読本 pp. 103〜108)
核スピン量子数 I と核スピン磁気量子数 mI (-I < mI < I) によって核スピンは記述される。
電子の場合と異なり, I は整数または半整数(つまり 0, 1/2, 1, 3/2, )の値を取りうる。この値は核種によって決まる。
)の値を取りうる。この値は核種によって決まる。
核磁気モーメント z 成分
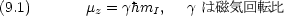
 N
N
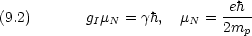
| 原子核 | 天然存在比 | スピン I | gI |
| 1H | 99.895 | 1/2 | 5.58536 |
| 2D | 9.65 ×10-3 | 1 | 0.857386 |
| 12C | 98.9 | 0 | − |
| 13C | 1.10 | 1/2 | 1.4044 |
| 14N | 99.634 | 1 | 0.40358 |
| 15N | 1.04 ×10-3 | 1/2 | -0.56608 |
| 16O | 99.96 | 0 | − |
| 17O | 0.038 | 5/2 | -0.7572 |
試料を静磁場中に置き電磁波をあてる。
電磁波の周波数は固定して,静磁場の大きさを連続的に変化させるとあるところで電磁波の吸収が起きる。そのときの共鳴条件は
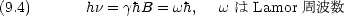
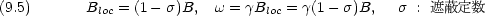
 は正(反磁性)の時も負(常磁性)のときもある。
は正(反磁性)の時も負(常磁性)のときもある。 を用いる。化学シフトは,標準物質の共鳴周波数を
を用いる。化学シフトは,標準物質の共鳴周波数を  o,共鳴の起きる磁場を Bo
として次のように定義される。
o,共鳴の起きる磁場を Bo
として次のように定義される。
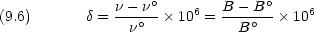
スピン  が外部磁場と平行であるとしたとき,
が外部磁場と平行であるとしたとき,  のスピンの個数 N
のスピンの個数 N と
と  スピンの個数 N
スピンの個数 N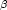 とは,平衡において次のような Boltzmann 分布をしていると考えられる。
とは,平衡において次のような Boltzmann 分布をしていると考えられる。
 スピン - スピン緩和 (横緩和)
スピン - スピン緩和 (横緩和) と
と 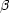 の数が平衡の Boltzmann 分布に戻っていく
の数が平衡の Boltzmann 分布に戻っていく スピン - 格子緩和 (縦緩和)
スピン - 格子緩和 (縦緩和)
| 原子核 | 1H | 2D | 12C | 13C | 14N |
| スピン I | 1/2 | 1 | 0 | 1/2 | 1 |
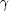 I I |
5.58536 | 0.857386 | − | 1.4044 | 0.40358 |