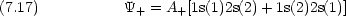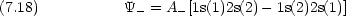7 電子スピン
電子の性質を考える上でスピンは重要な役割を果たす。電子スピンは,直感的には電子の自転としてとらえられるが,二つの方向しか取ることが出来ないなど,古典的な自転からは理解不可能な性質を持っている。
(副読本 pp. 88〜94)
7.1 Stern-Gerlach の実験
不均一磁場中に銀の原子線を通すと,磁気モーメントによって分裂が生じる。
電子の軌道角運動量から考えれば原子線は奇数本に分裂する事が期待されるが,実際には 2本に分裂する。
7.2 電子スピン
スピン角運動量演算子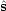 (軌道角運動量演算子と同じ交換関係)
(軌道角運動量演算子と同じ交換関係)
| |
演算子 |
量子数 |
固有値 |
固有関数 |
| 角運動量の 2 乗 |
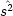 |
s = 1/2 |
s(s + 1)h2 |
 , ,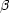
|
| 角運動量 z 成分 |
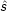 z z |
ms = 1/2 |
h/2 |
 |
| |
|
ms = -1/2 |
-h/2 |
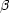 |
s はスピン量子数であり,電子の場合には必ず 1/2 という値を取る。
ms はスピン磁気量子数とよばれ-s < ms < s の値を取りうるが,電子の場合これは 1/2 または -1/2 である。
スピン波動関数  と
と 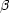 とは規格直交している。つまり
とは規格直交している。つまり
7.3 Pauli の原理
多電子系について「任意の一組の電子のラベルを交換すると全波動関数は符号を換える」
2 電子 2 準位モデル
基底状態
a の場合の波動関数
Pauliの原理を満たさないので,許されない
b の場合の波動関数は二種類考えられる
これら も, Pauli の原理を満たさないので,許されない。しかし,そもそも電子 1 と電子 2 は区別できないので, b の状態の波動関数は上のように書くことはおかしい。そこで 2 つの波動関数の線形結合を考える。
式 (7.6) は Pauli の原理を満たさないが,式 (7.7) は満たすのでこれだけが許される。
励起状態で許される波動関数
一重項
三重項
一重項よりは三重項が幾分安定
7.4 ベクトル模型
7.5 電子スピン共鳴Electron Spin Resonance (または電子常磁性共鳴EPR )
電子のスピン磁気モーメント
一様な磁場(磁束密度 B )中の電子スピンのエネルギー
縮退していた ms = ±1/2 の準位が磁場によって分裂
共鳴条件(振動数  の電磁波を吸収する条件)
ESR の測定では,通常
の電磁波を吸収する条件)
ESR の測定では,通常  を固定して, B を連続的に変化させる。
を固定して, B を連続的に変化させる。
不対電子を持つ分子の研究(ラジカル,遷移金属錯体,三重項)に応用可能である。
電子の感じている磁場は,巨視的磁場ではなく,局所磁場 Bloc
g は分子の電子構造に関係する。  は遮蔽定数
は遮蔽定数
超微細構造(核の磁気に関係)
演習問題
- 2 つの電子軌道だけが許されている系があるとする。エネルギーの低い準位の規格化された波動関数を
 A, 高い準位のものを
A, 高い準位のものを  B と書く。いまこの系に 2 つの電子が存在する。電子間反撥は無視する。
B と書く。いまこの系に 2 つの電子が存在する。電子間反撥は無視する。
- 基底状態の規格化された波動関数はどのようになるか。スピン部分を含めて述べよ。
- 第 1 励起状態の規格化された波動関数はどのようになるか。スピン部分を含めて述べよ。
- He の第一励起状態の波動関数は次のように書ける。
- なぜこのように書けると考えられるか述べよ。
- 規格化定数を計算せよ。
- 許される規格化されたスピン関数を書け。
- 電子間反撥を無視した場合のエネルギー期待値を計算せよ。
- 電子間反撥エネルギーを考慮した時,どちらのエネルギーが高いと考えられるか。
- 電子スピンについて。
- 電子スピンの磁気モーメントの z 成分は,スピン角運動量の z 成分とどのような関係にあるか。
- 一様な磁場(磁束密度 B )中の電子スピンのエネルギーはどのように書けるか。
- 電子スピン共鳴の共鳴条件について述べよ。
- 電子スピン共鳴はどのような分子の研究に適しているか。理由とともに述べよ。
- 分光計の周波数が 9.33 GHz であるとき,メチルラジカルの ESR スペクトルの中心が 329.4 mT にあった。 g はいくらか。
- ベンゼンカチオンは g = 2.00242 である。 9.33 GHz で動く ESR 装置における ESR 吸収の中心磁場強度を計算せよ。
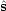 (軌道角運動量演算子と同じ交換関係)
(軌道角運動量演算子と同じ交換関係)
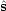 (軌道角運動量演算子と同じ交換関係)
(軌道角運動量演算子と同じ交換関係)
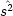
 ,
,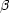
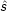 z
z 
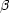
 と
と 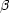 とは規格直交している。つまり
とは規格直交している。つまり
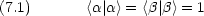
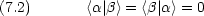
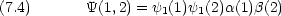
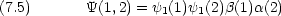
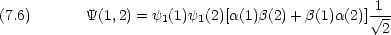
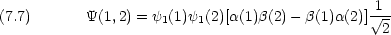
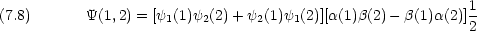
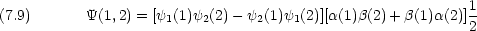
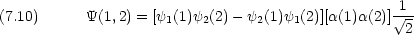
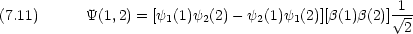
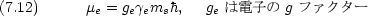
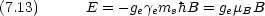
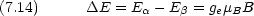
 の電磁波を吸収する条件)
の電磁波を吸収する条件)
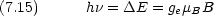
 を固定して, B を連続的に変化させる。
を固定して, B を連続的に変化させる。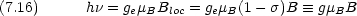
 は遮蔽定数
は遮蔽定数  A, 高い準位のものを
A, 高い準位のものを  B と書く。いまこの系に 2 つの電子が存在する。電子間反撥は無視する。
B と書く。いまこの系に 2 つの電子が存在する。電子間反撥は無視する。