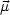 の磁石が作る磁場のポテンシャル
の磁石が作る磁場のポテンシャル  (
(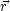 )
)
電子や原子核のスピンについて考察したり,各種の磁気共鳴現象を理解するための準備として,磁場について復習する。
(副読本 pp. 88〜94)
磁気モーメント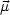 の磁石が作る磁場のポテンシャル
の磁石が作る磁場のポテンシャル  (
(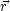 )
)
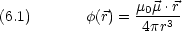
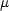 0 は真空の透磁率
0 は真空の透磁率
面積 A のループを流れる閉じた電流 I (法線ベクトル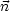 )による磁場のポテンシャル
)による磁場のポテンシャル  (
(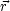 )
)
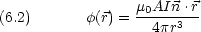

半径 R の円軌道 (A =  r2 ) を質量 me 電荷-e の粒子が角速度
r2 ) を質量 me 電荷-e の粒子が角速度  で運動するときの角運動量と電流
で運動するときの角運動量と電流
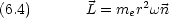
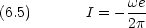
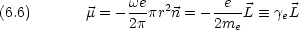
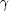 e は電子の磁気回転比という。
e は電子の磁気回転比という。
磁気量子数 m と軌道角運動量の z 成分との関係

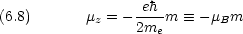
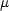 B をBohr 磁子という
B をBohr 磁子という
z 方向の均一磁場 B の中に置かれた磁気モーメントのエネルギー E
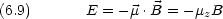
角運動量の z 成分が確定すると, x, y 成分は確定できないことに注意。
|
歳差運動
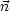 ) のつくる磁気モーメントはどのように表されるか。
) のつくる磁気モーメントはどのように表されるか。