多電子系を考える上での問題点は,電子間相互作用を考慮に入れなければならないというところにある。
Schr
 dinger 方程式の変数分離を可能にするには,電子間相互作用を無視するか,電子の感じる有効ポテンシャルを一電子の座標のみで表すような近似が必要である。
dinger 方程式の変数分離を可能にするには,電子間相互作用を無視するか,電子の感じる有効ポテンシャルを一電子の座標のみで表すような近似が必要である。(副読本 pp. 95〜102)
水素以外の原子は複数の電子を持っている。
多電子系を考える上での問題点は,電子間相互作用を考慮に入れなければならないというところにある。
Schr dinger 方程式の変数分離を可能にするには,電子間相互作用を無視するか,電子の感じる有効ポテンシャルを一電子の座標のみで表すような近似が必要である。
dinger 方程式の変数分離を可能にするには,電子間相互作用を無視するか,電子の感じる有効ポテンシャルを一電子の座標のみで表すような近似が必要である。
(副読本 pp. 95〜102)
N 電子系で,ハミルトニアンが次のような形に書ければ, Schr dinger 方程式は変数分離可能
dinger 方程式は変数分離可能
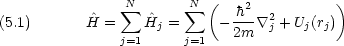
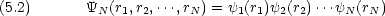
 j に適当な形を仮定。
j に適当な形を仮定。
 i から計算。
i から計算。
 jを再計算
jを再計算
 i とを計算。
i とを計算。
このようにして求めたポテンシャルをつじつまの合う場(自己無撞着場)とよぶ。のちに, Fock が電子スピンを考慮するために改良した。
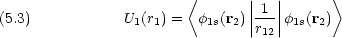
 1s は水素類似イオンの 1s 軌道の波動関数である。 U1(r1) は具体的にどのような形をしているか。
1s は水素類似イオンの 1s 軌道の波動関数である。 U1(r1) は具体的にどのような形をしているか。

これに基づいて, H から Ar までの原子の最外殻電子に対する有効核電荷を求めよ。