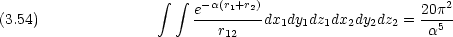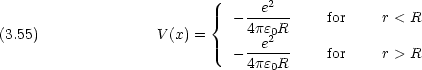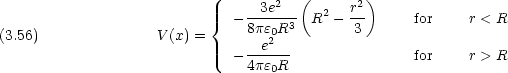dinger 方程式が変数分離不可能であり,厳密解は知られていない。
dinger 方程式が変数分離不可能であり,厳密解は知られていない。厳密に解けない問題に対しては種々の近似法が考案されている。この節ではよく用いられる近似法の一つである摂動法について述べる。(副読本 pp. 109 〜 128)
ヘリウム原子には 2 個の原子があり,電子間に反発力が働く。この場合は Schr dinger 方程式が変数分離不可能であり,厳密解は知られていない。
dinger 方程式が変数分離不可能であり,厳密解は知られていない。
厳密に解けない問題に対しては種々の近似法が考案されている。この節ではよく用いられる近似法の一つである摂動法について述べる。(副読本 pp. 109 〜 128)
次のように置いて得られる単位系を原子単位という。
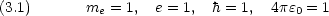
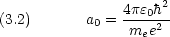
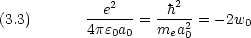
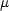
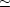 me と見なしたとき,ハミルトニアン
me と見なしたとき,ハミルトニアン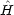 と Bohr 半径に相当する量 a 及び基底状態エネルギー W は au で次のように書ける。
と Bohr 半径に相当する量 a 及び基底状態エネルギー W は au で次のように書ける。
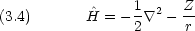

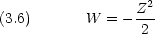
 dinger 方程式
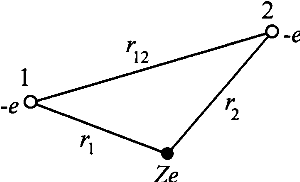
dinger 方程式 一般的に原子核の電荷数が Z で電子が 2 つある系について
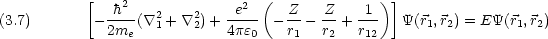
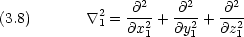 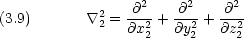 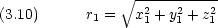 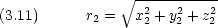 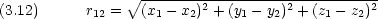 |
|
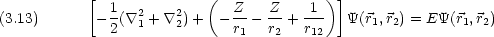
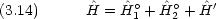
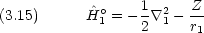
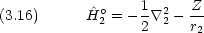
 dinger 方程式が変数分離できない。その結果方程式が解析的に解けない。
dinger 方程式が変数分離できない。その結果方程式が解析的に解けない。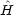 'の項がなければ,ハミルトニアンは水素類似原子のハミルトニアン
'の項がなければ,ハミルトニアンは水素類似原子のハミルトニアン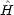 1 と
1 と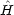 2 の重ね合わせであり,この場合容易に変数分離できて解が求められる。つまり,無摂動の Schr
2 の重ね合わせであり,この場合容易に変数分離できて解が求められる。つまり,無摂動の Schr dinger 方程式は
dinger 方程式は
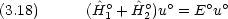
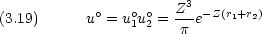
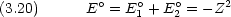
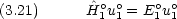
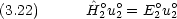
摂動法の一般論について述べる。次のような Schr dinger 方程式を解きたいが,解が解析的には求められないとする。
dinger 方程式を解きたいが,解が解析的には求められないとする。
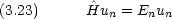
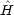 を二つの部分に分けて考える。
を二つの部分に分けて考える。
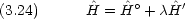
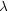 は無次元の小さい量で,最終的には
は無次元の小さい量で,最終的には 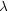 = 1 にするが,今のところ任意の数であると考えておく。
= 1 にするが,今のところ任意の数であると考えておく。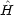 'は摂動のハミルトニア ンと呼ばれている。
'は摂動のハミルトニア ンと呼ばれている。
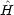 o は無摂動のハミルトニアンだが,これに対しては,固有関数 uno と固有値 Eno が既知であるとする。
o は無摂動のハミルトニアンだが,これに対しては,固有関数 uno と固有値 Eno が既知であるとする。
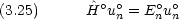
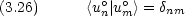
 に対して
に対して
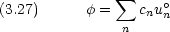
さて,摂動論では式 (3.23) の un と En とが次のように書けると仮定する。
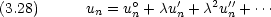
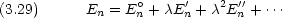
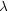 の次数ごとに整理する。
の次数ごとに整理する。
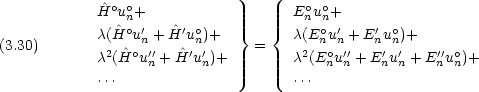
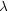 の任意の値に対して成立するためには,両辺で
の任意の値に対して成立するためには,両辺で 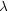 の各次数の係数がそれぞれ釣り合っていなければならない。
の各次数の係数がそれぞれ釣り合っていなければならない。
ゼロ次項(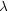 0 の係数)に関する方程式
0 の係数)に関する方程式
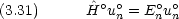
一次項(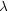 1 の係数)に関する方程式(一次摂動)は
1 の係数)に関する方程式(一次摂動)は
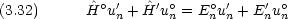
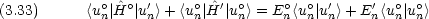
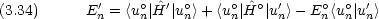
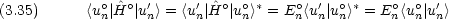
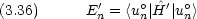
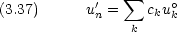
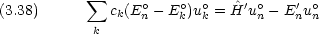
 dinger方程式を用いれば,次の式が得られる。
dinger方程式を用いれば,次の式が得られる。
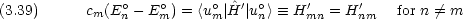
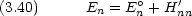
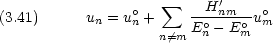
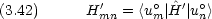
摂動論をヘリウム原子の基底状態エネルギーに応用する。
一般論で述べた式 (3.23) は,ヘリウム原子では式 (3.13) であから,ハミルトニアンは式 (3.14) 〜(3.17) で与えられ, 波動関数 un は  (
(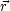 1,
1,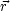 2) に相当する。
2) に相当する。
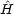 を (3.24) のように分離したとき,
を (3.24) のように分離したとき,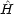 o は式 (3.15) と式 (3.16) の和 (
o は式 (3.15) と式 (3.16) の和 (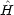 1o +
1o + 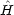 2o) で与えられ,
2o) で与えられ,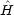 'は式 (3.17) で与えられる。 (3.25) に出てくる無摂動の波動関数 uno は式 (3.19) の uo,無摂動のエネルギー Eno は式 (3.20) の Eo である。
'は式 (3.17) で与えられる。 (3.25) に出てくる無摂動の波動関数 uno は式 (3.19) の uo,無摂動のエネルギー Eno は式 (3.20) の Eo である。
一次摂動のエネルギー E'は次の計算で与えられる。
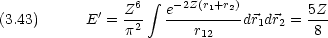
 1,
1,  2 のそれぞれについて,全空間にわたって行う。計算法は付録の第A-3章に示した。
2 のそれぞれについて,全空間にわたって行う。計算法は付録の第A-3章に示した。
基底状態エネルギーの数値計算結果(単位 eV )
| 無摂動 | 一次摂動 | 実験値 | |
| He | -108.24 | -74.42 | -78.62 |
| Li+ | -243.54 | -192.80 | -197.14 |
| Be2+ | -432.96 | -365.31 | -369.96 |
| B3+ | -676.50 | -591.94 | -596.40 |
| C4+ | -974.16 | -872.96 | -876.20 |
 o の固有値 Eno と固有関数
o の固有値 Eno と固有関数  no が既知であるとする。縮退はなく,
no が既知であるとする。縮退はなく, 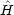 'で与えられるとする。
'で与えられるとする。
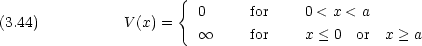
 dinger の方程式をたてて,エネルギー準位と波動関数とを求めよ。
dinger の方程式をたてて,エネルギー準位と波動関数とを求めよ。
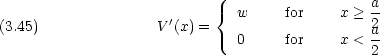
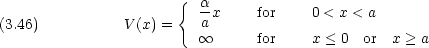
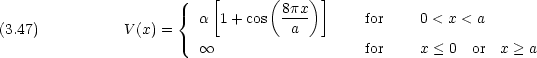
 電子系に対する自由電子モデルで,
電子系に対する自由電子モデルで,  系の両端に N がある場合に長さ a の箱の中の粒子の問題に次のような摂動を加えて考えることがある。
系の両端に N がある場合に長さ a の箱の中の粒子の問題に次のような摂動を加えて考えることがある。
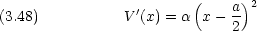
 電子が 2n 個ある系で,最長吸収波長はどのように表されるか。
電子が 2n 個ある系で,最長吸収波長はどのように表されるか。
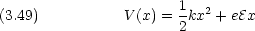

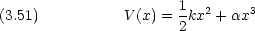
 は正の定数で,
は正の定数で,  の絶対値は小さいものとする。一次元調和振動子を無摂動系とする摂動法を用いて,基底状態と第一励起状態のエネルギーを
の絶対値は小さいものとする。一次元調和振動子を無摂動系とする摂動法を用いて,基底状態と第一励起状態のエネルギーを  に関して一次の項まで求めよ。
に関して一次の項まで求めよ。
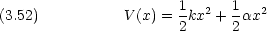
 は正の定数で,
は正の定数で,  の絶対値は小さいものとする。 k を力の定数とする一次元調和振動子が無摂動系であるとみなして,摂動法により基底状態と第一励起状態のエネルギーを
の絶対値は小さいものとする。 k を力の定数とする一次元調和振動子が無摂動系であるとみなして,摂動法により基底状態と第一励起状態のエネルギーを  に関して一次の項まで求めよ。結果 は厳密解と比較せよ。
に関して一次の項まで求めよ。結果 は厳密解と比較せよ。
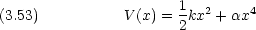
 は正の定数で,
は正の定数で,  の絶対値は小さいものとする。一次元調和振動子を無摂動系とする摂動法を用いて,基底状態と第一励起状態のエネルギーを
の絶対値は小さいものとする。一次元調和振動子を無摂動系とする摂動法を用いて,基底状態と第一励起状態のエネルギーを  に関して一次の項まで求めよ。
に関して一次の項まで求めよ。
 dinger方程式の解が既知であるとしたとき, He に対する無摂動のハミルトニアンはどのように選ぶのが便利か。
dinger方程式の解が既知であるとしたとき, He に対する無摂動のハミルトニアンはどのように選ぶのが便利か。