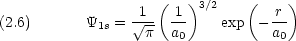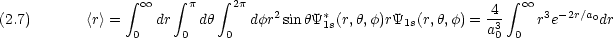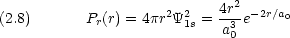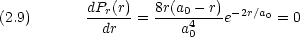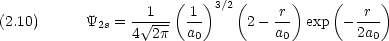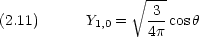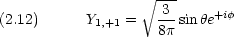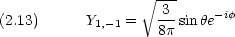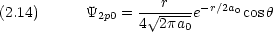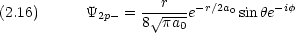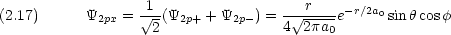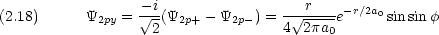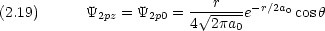2 水素原子の電子軌道
前章で得た水素原子の波動関数に基づいて,水素原子中の電子軌道について解説する。
(副読 本 pp. 78 〜87)
2.1 軌道と量子数
前節の結果から
| 主量子数 |
n = 1, 2, 3,  |
| 方位量子数 |
l = 0, 1, 2,  , n - 1 , n - 1 |
| 磁気量子数 |
m = -l, -l + 1,  , 0, , 0,  , l - 1, l , l - 1, l |
| 軌道 |
s 軌道 |
l = 0 |
|
p 軌道 |
l = 1 |
|
d 軌道 |
l = 2 |
|
 |
|
| 記号 |
1s, 2s, 2px, 2py, 2pz, 3s,  |
ある座標 (x,y,z) または (r, ,
, ) における電子の存在確率密度
) における電子の存在確率密度
この関数の意味は,微小体積 d = dxdydz = r2 sin
= dxdydz = r2 sin drd
drd d
d の中に電子を見いだす確率が P(r,
の中に電子を見いだす確率が P(r, ,
, )d
)d である,ということである。
である,ということである。
(確率密度 P(r, ,
, ) に体積 d
) に体積 d をかければ確率がでる。)
をかければ確率がでる。)
物理量 A の演算子をÂ とすると A の平均<A>は
一方,方向に関わりなく,原子核から r 〜 r + dr の間の位置に電子がいる確率は
もしも l = 0, m = 0 なら,  n,l,m(r,
n,l,m(r, ,
, ) は
) は  ,
,  に依存しない球対称な関数
に依存しない球対称な関数  (r) である。そのとき
(r) である。そのとき
ここで, 4 r2 は半径 r の球の表面積, 4
r2 は半径 r の球の表面積, 4 r2dr は内径 r 厚さ dr の非常に薄い球殻の体積である。
r2dr は内径 r 厚さ dr の非常に薄い球殻の体積である。
(ここでも,当然ながら,確率密度 P(r, ,
, ) に体積 d
) に体積 d をかければ確率がでる。)
をかければ確率がでる。)
2.2 s 軌道
l = 0 の場合 Y 0,0( ,
, ) =
) = 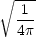 であり,波動関数は角度に依存しない。したがって,軌道は球対称である。
であり,波動関数は角度に依存しない。したがって,軌道は球対称である。
1s 軌道の波動関数
基底状態では 1s 軌道に 1 個の電子が入っている。
基底状態における電子と陽子の平均距離
ところで,
より,電子の存在確率が最も高い距離は r = a0
2s 軌道の波動関数
2s 軌道には 1s 軌道になかった節がある。つまり r = 2a0 のところで波動関数がゼロになる。
ns 軌道には (n - 1) 個の節がある
2.3 p 軌道
l = 1 では, Rn,1 が共通であるような 3 つの波動関数が考えられる。
エネルギーが等しい 3 つの軌道からなる。角運動量の z 成分が異なる。
2p 軌道の波動関数
p0 は z にダンベルを突き刺した形。 pア は z 軸の周りのドーナツで,右回りと左回り。
上に書いた形は,通常化学で用いる p 軌道の形と異なる。これは, p 軌道が 3 重に縮退していることと関係がある。 N重に縮退している軌道の波動関数は,一次独立で互いに直交している N 個の関数である。ところで,その N 個の関数の線形結合でできた関数は全て着目しているハミルトニアンの固有関数であり,同じエネルギー固有値を持っている。これは,一次独立で互いに直交している N 個の関数の組み合わせが無限に考えられることを意味している。つまり,縮退した準位の波動関数には,数学的に複数の表現があり,どれも同等の意味を持っている(どれが 正しいとか,どれが誤りということはない)。ただし,ある関数の「組み合わせ」を使うということが重要。水素原子の 2p 軌道の場合,式 (2.14) 〜 (2.16) の組み合わせが一つの可能性である。この組み合わせは,量子数 n, l, m の決め方から自然に導かれる。しかし,複素関数なので絵画的なイメージが描きにくく,化学結合の幾何学的な説明に用いるのには不便である。そこで,次のような関数を定義する。
式 (2.17) 〜 (2.19) の組み合わせが,化学でなじみ深い 2px, 2py, 2pz の表現である。
式 (2.14) 〜 (2.16) または式 (2.17) 〜 (2.19) のどちらの表現を用いても 2p 軌道には原点に節があることがわかる。
2.4 d 軌道
これにも 2 つの考え方がある
角運動量の z 成分による分類
d-2, d+2, d-1, d+1, d0
軌道の形による分類
dz2, dzx, dyz, dxy, dz2-y2
立体軌道図
図の上で、マウスの左ボタンを押しながらぐるぐる動かせます。
確率分布
演習問題
- 互いに直交している二つの規格化された波動関数
 (x) と
(x) と  (x) がある。
(x) がある。
どちらも同じハミルトニアン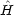 の固有関数であり,エネルギー固有値は E で等しい。
の固有関数であり,エネルギー固有値は E で等しい。
また, 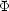 (x) = A[
(x) = A[ (x) +
(x) +  (x)] 及び
(x)] 及び  (x) = B[
(x) = B[ (x) -
(x) - (x)] で あるとする。ただし, A, B は定数である。
(x)] で あるとする。ただし, A, B は定数である。
 (x) と
(x) と  (x) とがそれぞれ規格化されているとはどういう意味か。式で表せ。
(x) とがそれぞれ規格化されているとはどういう意味か。式で表せ。
 (x) と
(x) と  (x) が直交しているとはどういう意味か。式で表せ。
(x) が直交しているとはどういう意味か。式で表せ。
 (x) と
(x) と  (x) とがそれぞれハミルトニアン
(x) とがそれぞれハミルトニアン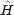 の固有関数であり,エネルギー固有値が E であるとはどういう意味か。式で表せ。
の固有関数であり,エネルギー固有値が E であるとはどういう意味か。式で表せ。
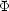 (x) と
(x) と  (x) がどちらも
(x) がどちらも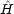 の固有関数であり,エネルギー固有値が E であることを示せ。
の固有関数であり,エネルギー固有値が E であることを示せ。
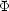 (x) と
(x) と  (x) とが直交していることを示せ。
(x) とが直交していることを示せ。
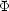 (x) と
(x) と  (x) とがそれぞれ規格化されているとして A, B を求めよ。
(x) とがそれぞれ規格化されているとして A, B を求めよ。
- 横軸に陽子からの距離 r をとって, 1s, 2s, 3s 軌道の波動関数をグラフに表せ。
- 水素原子の p 軌道の波動関数について。
- p+, p-, p0, px, py, pz のうち直交している組み合わせはどれか。
- p+, p-, p0, px, py, pz の角運動量 z 成分の期待値を求めよ。
- 2pz 軌道で電子を見いだす確率が最も高いのはどの位置か。
- 1s, 2s, 3s, 2pz の各軌道について,原子核の位置における電子の存在確率密度を計算せよ。
- 3s, 3pz の各軌道について,波動関数がゼロになる位置(節)を求めよ。
- 1s, 2s の各軌道について,半径 r から r + dr の球殻内に電子を見いだす確率が最も大きくなる r を求めよ。
- 水素原子について。
- n = 1 の場合に r, r2, r-1 の期待値を計算せよ。
- n = 2, l = 0 の場合に r, r2, r-1 の期待値を計算せよ。
- 水素原子中の電子の位置の期待値について。
- 2p+, 2p0, 2p- 軌道について r の期待値を計算せよ。
- p 軌道の r の期待値について次の式を導け。
- p 軌道の r の分散の期待値を表す式を導け。
- 水素原子中の電子の運動量の動径成分の演算子は次のように与えられる。
1s, 2s, 3s, 2pz の各軌道について, pr と pr2 の期待値を計算せよ。
- 1s, 2s, 3s, 2pz の各軌道について,陽子と電子の間に働く力の期待値を計算せよ。
- 光吸収による電子遷移について,遷移モーメント
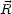 の x 成分は次のように与えられる。
の x 成分は次のように与えられる。
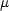 x は双極子モーメント
x は双極子モーメント 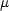 の x 成分, e は電気素量である。 y, z 成分も同様に書ける。
の x 成分, e は電気素量である。 y, z 成分も同様に書ける。
分子の場合には回転振動準位も関係するが,ここでは考えないことにする。
- 水素原子のエネルギー準位から Rydberg 定数を計算せよ。
- 1s
 2s の遷移は許されるか。ただし
2s の遷移は許されるか。ただし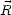 = 0 の遷移は許されない。
= 0 の遷移は許されない。
- 1s
 2px の遷移は許されるか。
2px の遷移は許されるか。
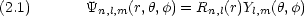
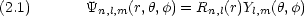

 , n - 1
, n - 1  , 0,
, 0,  , l - 1, l
, l - 1, l

 ,
, ) における電子の存在確率密度
) における電子の存在確率密度
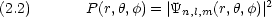
 = dxdydz = r2 sin
= dxdydz = r2 sin drd
drd d
d の中に電子を見いだす確率が P(r,
の中に電子を見いだす確率が P(r, ,
, )d
)d である,ということである。
である,ということである。 ,
, ) に体積 d
) に体積 d をかければ確率がでる。)
をかければ確率がでる。)
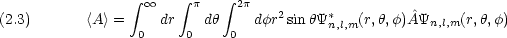
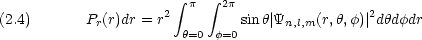
 n,l,m(r,
n,l,m(r, ,
, ) は
) は  ,
,  に依存しない球対称な関数
に依存しない球対称な関数  (r) である。そのとき
(r) である。そのとき
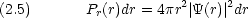
 r2 は半径 r の球の表面積, 4
r2 は半径 r の球の表面積, 4 r2dr は内径 r 厚さ dr の非常に薄い球殻の体積である。
r2dr は内径 r 厚さ dr の非常に薄い球殻の体積である。 ,
, ) に体積 d
) に体積 d をかければ確率がでる。)
をかければ確率がでる。)
 ,
, ) =
) = ![]() であり,波動関数は角度に依存しない。したがって,軌道は球対称である。
であり,波動関数は角度に依存しない。したがって,軌道は球対称である。