1 水素原子に対する波動関数
水素は陽子一つと電子一つのみからなるもっとも単純な原子である。
水素原子中の電子の運動に対する Schr dinger方程式については,厳密解がしられており,原子の電子構造を考える上での基礎になっている。
dinger方程式については,厳密解がしられており,原子の電子構造を考える上での基礎になっている。
(副読本 pp. 78 〜87)
1.1 水素原子に対するSchr dinger 方程式
dinger 方程式
Schr

dinger 方程式の極座標表示
換算質量
1.2 変数分離
波動関数  を動径部分 R(r) と角度部分 Y (
を動径部分 R(r) と角度部分 Y ( ,
, ) に分離する。
) に分離する。
左辺はr のみ,右辺は  ,
,  のみの関数なので,両辺は定数
のみの関数なので,両辺は定数 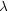 に等しいはずである。
に等しいはずである。
1.3 角度部分の波動関数
角度部分の Schr dinger 方程式は,二原子分子の回転運動に対する方程式と全く同じである。
dinger 方程式は,二原子分子の回転運動に対する方程式と全く同じである。
したがって答えも同じでなければならない。(物理化学 III のプリント参照)
ただし
l (= 0,1,2, ) は方位量子数と呼ばれ,電子の軌道角運動量の二乗 L2 に関係している。
m (-l < m < l) は磁気量子数と呼ばれ,電子の軌道角運動量の z 成分 Lz に関係している。
) は方位量子数と呼ばれ,電子の軌道角運動量の二乗 L2 に関係している。
m (-l < m < l) は磁気量子数と呼ばれ,電子の軌道角運動量の z 成分 Lz に関係している。
1.4 動径部分の波動関数
動径部分の波動関数は次のように与えられる。(補足A-1 参照)
Lks(x)は Laguerre の陪多項式と呼ばれ,次式で与えられる。
n (= 1, 2,  ) は主量子数と呼ばれ,電子のエネルギー準位 En に関係している。
方位量子数 l は 0 < l < n - 1 の間の値しかとることができない。
) は主量子数と呼ばれ,電子のエネルギー準位 En に関係している。
方位量子数 l は 0 < l < n - 1 の間の値しかとることができない。
演習問題
- 陽子 1 つと電子 1 つからなる系について。
- 全体の Schr
 dinger 方程式をかけ。
dinger 方程式をかけ。
- 重心運動と相対運動の部分に分離せよ。
- 相対運動の部分を極座標で表せ。
- R10 と R31 とが実際に水素原子の波動関数に対する Schr
 dinger 方程式の動径部分を満足することを示せ。
dinger 方程式の動径部分を満足することを示せ。
- 水素と重水素で基底状態エネルギーは何 cm-1 違うか。
- 水素原子の n = 1 の状態について。
- 電子が Bohr 半径以内にいる確率を計算せよ。また Bohr 半径の 2倍以内の場合も計算せよ。
- その距離以内に電子を見いだす確率が 90 % であるような距離を計算せよ。
- 水素原子の主量子数 n が 1 から 3 までの全ての定常状態について。
- 波動関数を書き下せ。
- エネルギー,角運動量の絶対値,角運動量の z 成分を書け。
- ポテンシャルエネルギーの期待値を計算せよ。
- 運動エネルギーとポテンシャルエネルギーとの間にはどのような関係があるか。これは,量子力学的ヴィリアル定理の一例である。
- He+, Li2+ 等は,水素原子と比較すると原子核の電荷が異なるだけで構成は同じであるため,水素類似原子(イオン)と呼ばれている。原子核の電荷数を Z としてこれらのイオンの定常状態の波動関数とエネルギー準位とを書け。
- ポジトロニウムは電子と陽電子とからなる。陽電子の質量は電子と等しく,電荷の絶対値は電子と等しいが符号は反対である。
- 換算質量を計算せよ。
- Bohr 半径に相当する半径を計算せよ。
- 基底状態エネルギーを計算せよ。
- n = 2 の軌道から n = 1 の軌道への遷移に伴って放出される電磁波の波長を計算せよ。
- 次のような三次元ポテンシャル中の質量 m の粒子の運動について。
- Schr
 dinger 方程式を書け。
dinger 方程式を書け。
- 変数分離して波動関数とエネルギー準位を求めよ。 P(r) = rR(r) を使え。
- 陽子と電子が三次元空間ではなく二次元平面上のみを運動するとした場合について。
- Schr
 dinger 方程式を書け。
dinger 方程式を書け。
- 変数分離して波動関数とエネルギー準位を求めよ。
- 平面上の軌道のみを電子が運動する Bohr モデルの妥当性について考察せよ。
 dinger方程式については,厳密解がしられており,原子の電子構造を考える上での基礎になっている。
dinger方程式については,厳密解がしられており,原子の電子構造を考える上での基礎になっている。 dinger方程式については,厳密解がしられており,原子の電子構造を考える上での基礎になっている。
dinger方程式については,厳密解がしられており,原子の電子構造を考える上での基礎になっている。 dinger 方程式
dinger 方程式 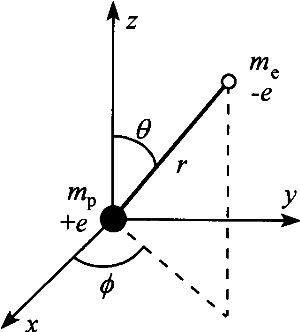
 dinger 方程式の極座標表示
dinger 方程式の極座標表示
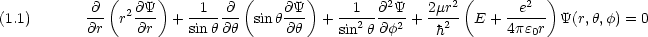
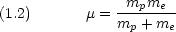
 を動径部分 R(r) と角度部分 Y (
を動径部分 R(r) と角度部分 Y ( ,
, ) に分離する。
) に分離する。
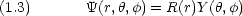
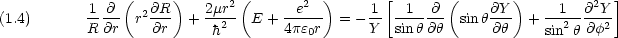
 ,
,  のみの関数なので,両辺は定数
のみの関数なので,両辺は定数 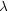 に等しいはずである。
に等しいはずである。
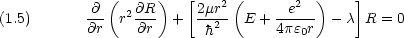
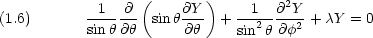
 dinger 方程式は,二原子分子の回転運動に対する方程式と全く同じである。
dinger 方程式は,二原子分子の回転運動に対する方程式と全く同じである。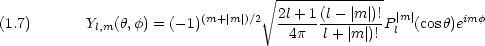
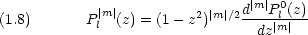

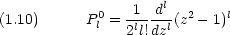
 ) は方位量子数と呼ばれ,電子の軌道角運動量の二乗 L2 に関係している。
) は方位量子数と呼ばれ,電子の軌道角運動量の二乗 L2 に関係している。
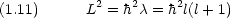
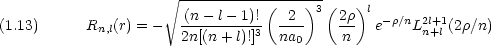

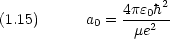
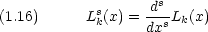
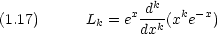
 ) は主量子数と呼ばれ,電子のエネルギー準位 En に関係している。
) は主量子数と呼ばれ,電子のエネルギー準位 En に関係している。
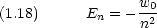
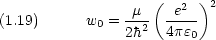
 dinger 方程式をかけ。
dinger 方程式をかけ。
 dinger 方程式の動径部分を満足することを示せ。
dinger 方程式の動径部分を満足することを示せ。
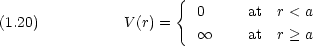
 dinger 方程式を書け。
dinger 方程式を書け。
 dinger 方程式を書け。
dinger 方程式を書け。