A-12 前期量子論
古典物理学では説明のできない現象のひとつに,原子スペクトルがある。
大胆な仮説に基づい て原子スペクトルを説明したのが Bohr のモデルである。
Bohr のモデルのように,「量子条件」 という天下りの仮定をおいて,古典物理学の問題点を克服しようとした理論を前期量子論という。
A-12.1 原子スペクトル
放電管を希薄な水素ガスでみたし高電圧をかけると光を発する。
水素原子が発する光は,太陽光線のようにあらゆる波長の光が混じり合ったもの(連続スペクトル)ではなく,
ある特定の波長の光のみからなる(不連続スペクトル)ことがわかった。
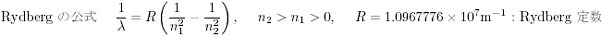
A-12.2 原子模型
| J. J. Thomson |
正電荷が原子いっぱいに均一分布 |
| H. Nagaoka |
土星型 |
A-12.3 α粒子の散乱と Rutherford の実験
10-10 m 原子の大きさの中で 10-15 m に正電荷が集中
Nagaoka-Rutherford 模型の問題点
円運動する粒子は常に加速度を持つ
電磁気学 加速度運動する荷電粒子
加速度運動する荷電粒子
 電磁波を放出(連続スペクトル)
電磁波を放出(連続スペクトル)  安定に存在し得ない
安定に存在し得ない
A-12.4 粒子の等速円運動
二次元平面内で円運動する粒子を考える 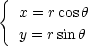
r は固定されていて  だけが変化する。角速度
だけが変化する。角速度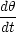 =
= 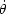 =
=  = const. として
= const. として
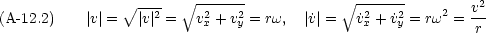
角速度一定でも常に円の中心に向かう方向に加速度がかかる
遠心力はこの加速度の符号を変えて粒子の質量をかけたもの
A-12.5 Bohr のモデル
A-12.5.1 Bohr の量子条件
Bohr の仮説
- 原子は任意の値のエネルギーをとれるのではない。定常状態であるエネルギー準位が存在し,その状態では原子は光を放射しない。
-
原子はある定常状態から別の定常状態に遷移するときに電磁波(光)を吸収(放出)する
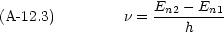
Bohr の量子条件 「円運動する粒子の角運動量は h(= h/2 ) の整数倍でなければならない」
) の整数倍でなければならない」
A-12.5.2 水素原子
電荷 +e の陽子が静止しており,その周囲を質量 me 電荷-e の電子が等速円運動する
遠心力と Coulomb 力がつりあう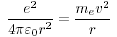
Bohr 条件を入れる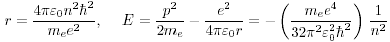
Bohr 半径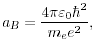 , Rydberg 定数
, Rydberg 定数 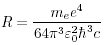
A-12.6 Sommerfeld の量子条件
Bohr の条件を等速円運動以外に一般化
一般化運動量 p と一般化座標 q (例えば運動量と座標,角運動量と角度)
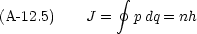
J : 作用
演習問題
- 半径 r の円軌道を等速円運動する質量 m の粒子について次の量を求めよ。
(1) 運動量の x 成分
(2) 加速度の大きさと方向
(3) 角運動量
(4) 運動エネルギー
(5) 慣性モーメント
- 水素原子を,固定された原子核(電荷 e )の周囲の円軌道を運動する電子(電荷-e, 質量 me )とみなす。 Bohr モデルから次の量を計算せよ。
- 軌道の半径。
- エネルギー準位。
- 第一励起状態状態から基底状態への遷移に伴う放射の振動数,波数,波長。
- 基底状態の水素原子をイオン化するのに必要なエネルギー。
- Bohr モデルの水素原子について次の量を計算せよ。
- 量子数 n の時の電子の速さを表す式。
- 基底状態における電子の速さの数値。
- 基底状態における電子の物質波の振動数,波数,波長の数値。
- 粒子の速度が光速に近くなると相対論的な効果を無視することが出来ない。
Bohr モデルの基底状態にある水素原子の電子に対して相対論的効果を無視するのは妥当かどうか論じよ。
- 陽子の周りの円軌道を回転する電子について,両者の引力がクーロン力ではなく万有引力のみである時の Bohr 半径を求めよ。
万有引力定数 G = 6.673 ×10-11 m3 s-2 kg-1
- 太陽の質量は 1.971 × 1030 kg,地球の質量は 5.983 × 1024 kg,太陽と地球との距離は 1.497 × 1011 m,
万有 引力定数 G = 6.673 × 10-11 m3 s-2 kg-1 である。地球は円軌道を運動しているとして Bohr モデルで考える。
- エネルギー準位の表式を求めよ。
- 距離の実測値から量子数を見積もれ。
- その付近で量子数を 1 だけ変化させるのに必要なエネルギーを見積もれ。
-
水素の原子スペクトルの波長は次の Rydberg の公式で表される。
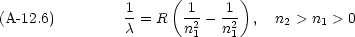
ただし, R は Rydberg 定数で実験的に 1.0967776 × 10
7 m
-1 である。
- Lyman 系列(n1 = 1)の最初の 4 つのスペクトルの波長を求めよ。
- Balmer 系列(n1 = 2)の最初の 4 つのスペクトルの波長を求めよ。
- Paschen 系列(n1 = 3)の最初の 4 つのスペクトルの波長を求めよ。
- Bracket 系列(n1 = 4)の最初の 4 つのスペクトルの波長を求めよ。
- Pfund 系列(n1 = 5)の最初の 4 つのスペクトルの波長を求めよ。
- 水素原子を,固定された核(電荷 e )の周囲の円軌道を運動する電子(電荷-e , 質量 me )とみなし, Bohr モデルから Rydberg 定数を計算せよ。
- 前問で求めた Rydberg 定数の理論値と実験値のずれはどの程度か。また何に由来するか。
- 観測された原子スペクトルと古典物理学との矛盾について述べよ。
- He+ イオンを,固定された原子核(電荷 2e )の周囲の円軌道を運動する電子とみなす。 Bohr モデルから次の量を計算せよ。
- 基底状態における軌道の半径。
- 基底状態エネルギー。
- 前 2 問の結果を水素原子の場合と比較せよ。核電荷数によってどのように変化したか。
- He+ イオンの原子スペクトルについて Bohr モデルで考える。
- Rydberg 定数に相当する量を求めよ。
- 高い準位から n = 4 の準位への遷移に伴うスペクトルは Pickering 系列と呼ばれている。最初の 4 つのスペクトルの波長を計算せよ。
- 前 2 問の結果を水素原子の場合と比較せよ。核電荷数によってどのように変化したか。
- 電荷 Ze の原子核と 1 つの電子から構成されるイオンを水素類似(原子)イオンという。 Bohr モデルから水素類似イオンの軌道半径とエネルギー準位を求めよ。
- 長さ r の質量のない棒の両端にそれぞれ質量 m1, m2 の粒子がとりつけられているとする。
- 重心から m1 までの距離 r1 と,重心から m2 までの距離 r2 とを求めよ。
- 重心を通り棒に垂直な方向の回転軸の周りを角速度
 で回転するとする。 m1, m2 の速さはどれだけか。
で回転するとする。 m1, m2 の速さはどれだけか。
- 系の運動エネルギーを
 を使って表せ。
を使って表せ。
-
運動エネルギー K が次式で表されるとする。

慣性モーメント I はどのように定義されるか。
- この運動を,固定点の周囲の半径 r の円軌道を運動する粒子の運動と同様の方程式で取り扱おうとしたとき,質量の代わりに用いる換算質量
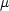 はどのようになるか。
はどのようになるか。
- 水素原子の Bohr モデルで,電子の質量の代わりに陽子と電子の換算質量を用いた場合,次の量はどのような値を持つか。
- 基底状態の Bohr 半径。
- Rydberg 定数。
- イオン化エネルギー。
- ミューオンは電子と同じ電荷を持ち電子の 207 倍の質量を持つ素粒子である。陽子とミューオンとは,ミューオン原子と呼ばれる短寿命の化学種を構成する。 Bohr モデルからミューオン原子の軌道半径とエネルギー準位を求 めよ。
- 窒素分子について。
- 換算質量を計算せよ。ただし両方の窒素原子の原子量は 14.00 とする。
- 原子間距離は 0.1097 nm であるとする。重心周りの慣性モーメントはどれだけか。
- 角速度が
 である時の角運動量と運動エネルギーをかけ。
である時の角運動量と運動エネルギーをかけ。
- 角運動量に対する Bohr の量子条件から,回転のエネルギー準位を導け。
- 第一励起状態状態から基底状態への遷移に伴う放射の振動数,波数,波長を計算せよ。
- HCl 分子について。
- 換算質量を計算せよ。 H の原子量は 1.008, Cl の分子量は 34.97 とする。
- 原子間距離は 0.1275 nm である。重心周りの慣性モーメントはどれだけか。
- 第一励起状態状態から基底状態への遷移に伴う放射の振動数,波数,波長を計算せよ。
- 水素原子に対する Bohr の量子条件が Sommerfeld の量子条件と同一であることを示せ。
- 時間の単位 1 s は,セシウム -133 原子の基底状態超微細構造間の遷移に対応する放射の 9192631770 周期の継続時間と定義されている。基底状態超微細構造間のエネルギー差はどれだけか。
-
次の一次元ポテンシャル V (x) の中を質量 m の粒子が運動する。
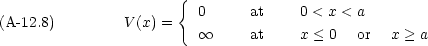
Sommerfeld の量子条件を適用してエネルギー準位を計算せよ。
- 次の一次元ポテンシャル
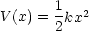 の中を質量 m の粒子が運動する。 k は力の定数と呼ばれる定数である。 Sommerfeld の量子条件を適用してエネルギー準位を計算せよ。
の中を質量 m の粒子が運動する。 k は力の定数と呼ばれる定数である。 Sommerfeld の量子条件を適用してエネルギー準位を計算せよ。
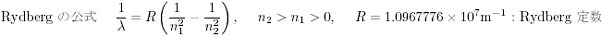
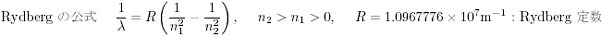
 加速度運動する荷電粒子
加速度運動する荷電粒子  電磁波を放出(連続スペクトル)
電磁波を放出(連続スペクトル)  安定に存在し得ない
安定に存在し得ない
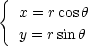
 だけが変化する。角速度
だけが変化する。角速度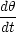 =
= 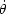 =
=  = const. として
= const. として
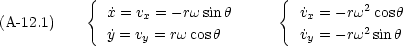
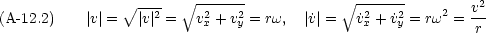
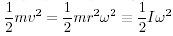
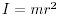
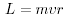
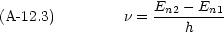
 ) の整数倍でなければならない」
) の整数倍でなければならない」
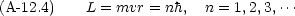
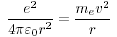
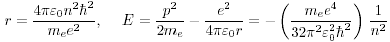
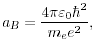 , Rydberg 定数
, Rydberg 定数 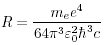
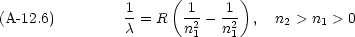
 で回転するとする。 m1, m2 の速さはどれだけか。
で回転するとする。 m1, m2 の速さはどれだけか。
 を使って表せ。
を使って表せ。

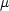 はどのようになるか。
はどのようになるか。
 である時の角運動量と運動エネルギーをかけ。
である時の角運動量と運動エネルギーをかけ。
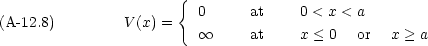
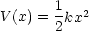 の中を質量 m の粒子が運動する。 k は力の定数と呼ばれる定数である。 Sommerfeld の量子条件を適用してエネルギー準位を計算せよ。
の中を質量 m の粒子が運動する。 k は力の定数と呼ばれる定数である。 Sommerfeld の量子条件を適用してエネルギー準位を計算せよ。