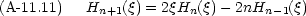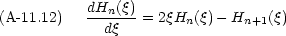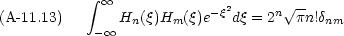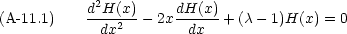
次のような微分方程式を Hermite の微分方程式という。
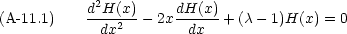
これを解くために, H(x) が次のような形に書けると仮定する。
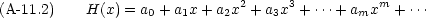
H(x) の微分を級数で書いてみる
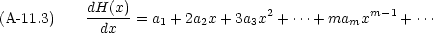
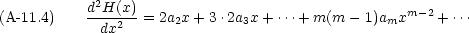
| 2a2 | +6a3x | +12a4x2 | + |
+(m - 2)(m - 1)am+2xm | + |
|
| -2a1x | -4a2x2 | + |
-2mamxm | - |
||
+( - 1)a0 - 1)a0 |
+( - 1)a1x - 1)a1x |
+( - 1)a2x2 - 1)a2x2 |
+ |
+( - 1)amxm - 1)amxm |
- |
= 0 |
全ての m にたいして xm の係数がゼロでなければならないから, am は次の漸化式を満たす。
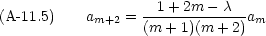
 が次のような値をとらなければならない
が次のような値をとらなければならない
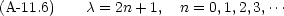
指数関数の Taylor 展開を利用すると次の式が得られる。
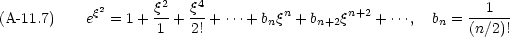
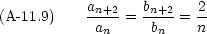
これは,この二つの関数が同程度に発散する事を意味している。
ただし一般には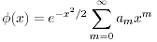 は発散する
は発散する
無限級数ではなく途中で切れるようにすると e-x2/2 をかければ|x|
 で必ず波動関数がゼロになる
で必ず波動関数がゼロになる
Hermite 多項式は次の式から計算することもできる。
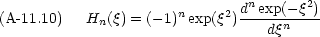
Hermite 多項式には次のような性質がある。