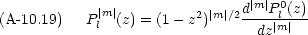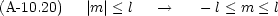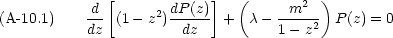
次のような方程式を Legendre 方程式という。
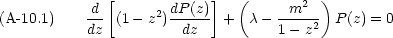
初めに m = 0 の場合を考える(Legendre の微分方程式)
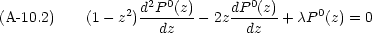
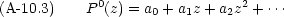
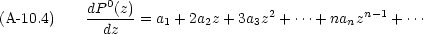
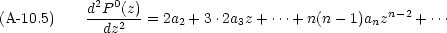
| 2a2 | +6a3z | +12a4z2 | + |
+(n + 2)(n + 1)an+2zn | + |
|
| -2a2z2 | - |
-n(n - 1)anzn | - |
|||
| -2a1z | -4a2z2 | - |
-2nanzn | - |
||
+ a0 a0 |
+ a1z a1z |
+ a2z2 a2z2 |
+ |
+ anzn anzn |
- |
= 0 |
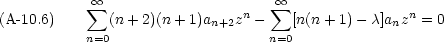
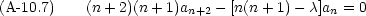
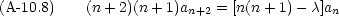
 を選ぶ
を選ぶ
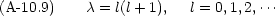
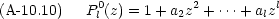
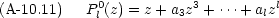
この多項式 Pl0(z) は次の Rodrigues の公式から作ることもできる
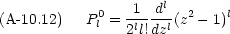
次に m 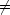 0 の場合を考える
0 の場合を考える
m = 0 の Legendre 方程式を|m|回微分する
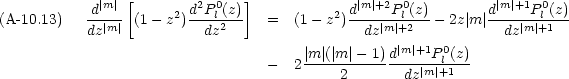
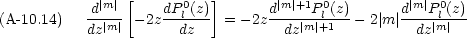
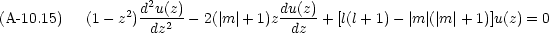
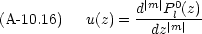
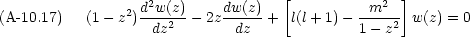
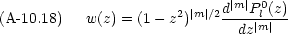
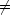 0 の場合,次の多項式が目的の方程式を満たす
0 の場合,次の多項式が目的の方程式を満たす