|
極座標は,ベクトルを大きさと基準軸からの角度で表現する座標系である。
|
まず,速度ベクトル r の大きさは r である。そして, z 軸と r とのなす角を  とする。
とする。
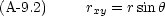
 とする。
とする。
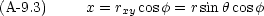
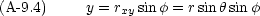
変数の範囲は


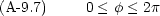
次に, r,  ,
,  を x, y, z で表しておく。
を x, y, z で表しておく。

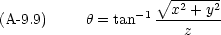
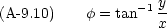
これを用いて前節の計算を行う。すなわち
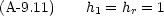
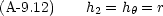
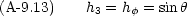
この d については,次のような考え方もできる。
については,次のような考え方もできる。
d は,位置を (dr, d
は,位置を (dr, d ,d
,d ) 変化させてできる直方体の体積である。
) 変化させてできる直方体の体積である。
dr の変化に対しては,辺の長さはそのまま dr である。
しかし, d の変化に対しては,辺の長さは rd
の変化に対しては,辺の長さは rd となるはずである。ここで
となるはずである。ここで  はラジアンを単位にしている。
はラジアンを単位にしている。
また, d の変化に対しては,辺の長さは sin
の変化に対しては,辺の長さは sin d
d である。このような三辺を持つ直方体が d
である。このような三辺を持つ直方体が d = dxdydz に対応しているはずである。
= dxdydz に対応しているはずである。
直方体の体積から式 (A-9.14) がでる。
|
さて,ベクトルの微分演算子は次のようになる。
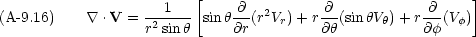
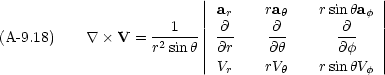
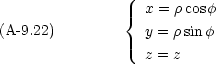
 ,
,  はどのような範囲の値をとるか。
はどのような範囲の値をとるか。
 はなにに等しいか。
はなにに等しいか。
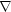 はどのようにかけるか。
はどのようにかけるか。
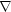 2 はどのようにかけるか。
2 はどのようにかけるか。