 (q1,q2,q3) の座標変換を考える。 x, y, z 方向の単位ベクトルを i, j, k とする。例えば x は q1, q2, q3
の関数として表すことが出来るから
(q1,q2,q3) の座標変換を考える。 x, y, z 方向の単位ベクトルを i, j, k とする。例えば x は q1, q2, q3
の関数として表すことが出来るから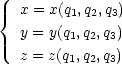 あるいは
あるいは 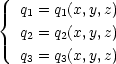
方向を表す単位ベクトル ai (i = 1,2,3) は, qi = const. の面に垂直で qi の増加する方向にとる。
dx は次のようになる。(dy, dz も同様に書ける)
(x,y,z)  (q1,q2,q3) の座標変換を考える。 x, y, z 方向の単位ベクトルを i, j, k とする。例えば x は q1, q2, q3
の関数として表すことが出来るから
(q1,q2,q3) の座標変換を考える。 x, y, z 方向の単位ベクトルを i, j, k とする。例えば x は q1, q2, q3
の関数として表すことが出来るから
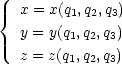 あるいは
あるいは 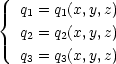
方向を表す単位ベクトル ai (i = 1,2,3) は, qi = const. の面に垂直で qi の増加する方向にとる。
dx は次のようになる。(dy, dz も同様に書ける)
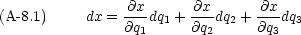
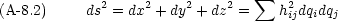
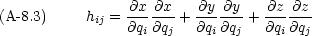
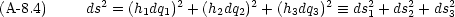
 は
は
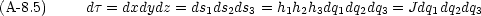

スカラー関数  (x,y,z) がある時その勾配は次のベクトル関数 grad
(x,y,z) がある時その勾配は次のベクトル関数 grad である。
である。
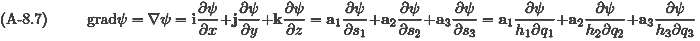
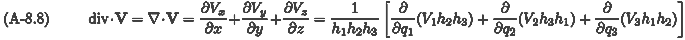
 とすれば Laplacian の表式を得る。
とすれば Laplacian の表式を得る。
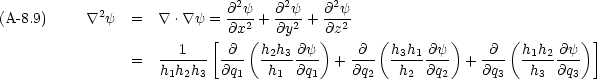
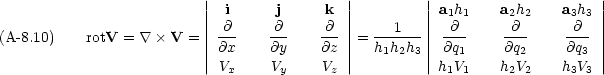
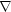 はどのようにかけるか。
はどのようにかけるか。
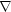 2 はどのようにかけるか。
2 はどのようにかけるか。
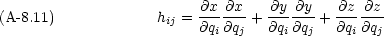
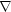 はどのようにかけるか。
はどのようにかけるか。
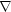 2 はどのようにかけるか。
2 はどのようにかけるか。