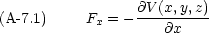
話を簡単にするため,質量 m の質点 1 つが,ポテンシャルエネルギー V (x,y,z) の空間中にある場合を考える。粒子にかかる力 F はポテンシャルのみで決まる。
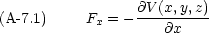
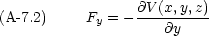
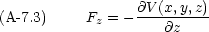
ここで, Lagrangian L を次のように定義する。
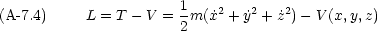
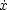 = vx である。この関数 L を使えば, Newton の運動方程式 F = ma は次のように書き直すことができる。
= vx である。この関数 L を使えば, Newton の運動方程式 F = ma は次のように書き直すことができる。
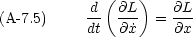
この方程式の意味するところを,一次元で説明する。
時刻 t1 に x1 にあった粒子が時刻 t2 に x2 にあるとする。では,途中の時間ではどのような道筋をたどるのか。
それは,次の積分 I が極小になるような道筋である。
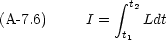
さて, Lagrangian L は,一次元でいえば x と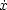 = vx とが独立変数であるような関数である。よって, L の全微分dL は
= vx とが独立変数であるような関数である。よって, L の全微分dL は
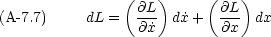
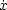 とすれば
とすれば
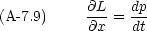
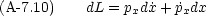
L の代わりに, x と px とが独立変数であるような関数 H を考えよう。それは次のようにすれば作れる。
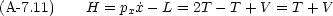
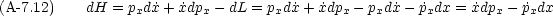
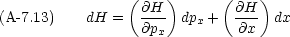
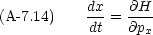
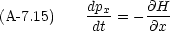
このような,形をした方程式の組を正準方程式といい,正準方程式を満たす変数の組(この場合 x と px)は,互いに正準共役であるという。
また, H は Hamiltonian という。ここで考えているような例の場合, H は全エネルギーに他ならない。
正準方程式を用いた Hamilton 形式の解析力学は,それ自体が便利だということは特にないが,量子力学が形成される上で,重要な役割を果たした。
座標変換を施しても,新しい変数 qr と pr とが正準方程式を満たすように変換することができる。このような変数変換を正準変換という。例えば,ポテンシャルエネルギーが原点からの距離 r のみで決まるような場合,極座標を使うのが 便利だが,その場合の Hamiltonian は次のように書ける。
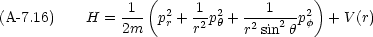
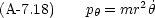
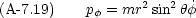
 と p
と p ,
,  と p
と p がそれぞれ正準方程式を満たすことはすぐに示すことができる。
がそれぞれ正準方程式を満たすことはすぐに示すことができる。
この Hamiltonian は  に依存しない。このような場合
に依存しない。このような場合  は循環座標であるという。
は循環座標であるという。
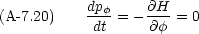
 が一定であることがすぐに解る。
が一定であることがすぐに解る。
今までの議論では,時間 t は,他の変数(座標と運動量)とは別に,特別な扱いを受けている。
それをやめるにはどうすればよいか。
では,エネルギーも座標と運動量で決まる Hamiltonian ではなく, E というエネルギーが独立変数であるとする。
そして,次のような新しい関数 F を定義する。
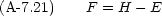
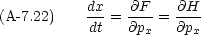
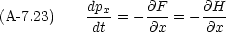
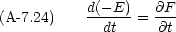
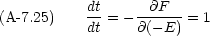
 と p
と p ,
,  と p
と p の場合も示せ。
の場合も示せ。
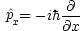 と書ける。
と書ける。