A-6 一次結合・一次独立・一次従属

A-6.1 一次結合

関数 f1, f2, f3, ..., fn の一次結合とは， c1, c2, c3, ..., cn を定数として

A6-1
一次結合は線形結合ともいう

A-6.2 一次独立・一次従属

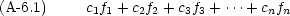
関数 f1, f2, f3, ..., fn が与えられているとき，次の方程式を考える

A6-2
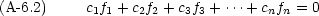
ここで c1 = c2 = c3 = ... = cn = 0 が唯一の解であるとき， f1, f2, f3, ..., fn は一次独立であるという。
またそれ以外の解がある場合，一次従属であるという。

一次独立・一次従属はそれぞれ線形独立・線形従属ともいう

A-6.3 n 階線形微分方程式

一般に，関数 y とその導関数 y', y”, y(3), ..., y(n) についての一次方程式

A6-3
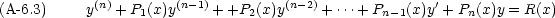
を n 階線形微分方程式という。ここで P1(x), P2(x), ..., Pn(x), R(x) は既知の関数である。

特に R(x) = 0 の場合を斉次方程式という。

定理 u1(x), u2(x), ..., un(x) が n 階斉次線形微分方程式の n 個の一次独立な解ならば，その方程式の一般解は

A6-4
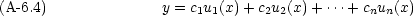
と表される。ただし c1, c2, c3, ..., cn は任意定数である。

時間に依存しない Schrdinger 方程式は普通 2 階斉次線形微分方程式である。

演習問題

  1. 次に示す関数の組は一次独立か一次従属か述べよ。
    1. sinx,    sin2x,    sin3x,    sin4x
    2. cosx,    cos2x,    cos3x,    cos4x
    3. sinx,    cosx,    sin2x,    cos2x
    4. eix,    e2ix,    e3ix,    e4ix
    5. eix,    e-ix,    e2ix,    e-2ix
    6. sinx,    cosx,    eix,    e-ix