A-5 複素数

A-5.1 複素数

虚数単位   i = V~ --- -1
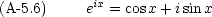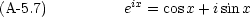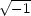
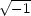
a, b を実数とするとき，次のような数 c を複素数という。    c = a + ib

複素数 c の実部 Re(c) = a
複素数 c の虚部 Im(c) = b
複素数 c の共役複素数 c* = a - ib

2 つの複素数 c = a + ib と z = s + it とは， a = s かつ b = t の時に限って等しい。これを c = z と表す。

A-5.2 複素数の演算

i をあたかも代数における文字のように取り扱い， i2 が現れたならばこれを-1 で置き換える。
四則演算

A5-1
A5-2

A5-3

A-5.3 複素数の絶対値

A5-4
すると
A5-5

　

A-5.4 Euler の公式

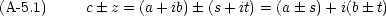
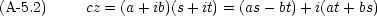
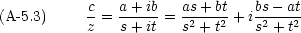
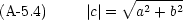
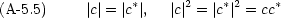
指数関数の Taylor 展開を使えば下の等式を示すことが出来る。

A5-6

演習問題

  1. Taylor 展開を用いて次の Euler の公式が正しいことを示せ。
    A5-7
  2. Euler の公式を用いて三角関数の加法定理を導け。