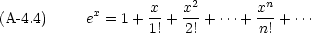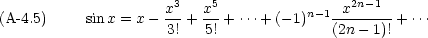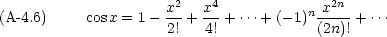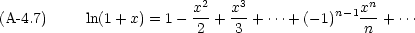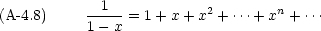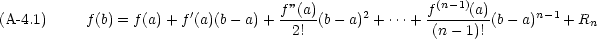
ここで
関数 f(x) が a < x < b を含むある区間で n- 1 回微分可能で, f(x) の n- 1 次導関数 f(n-1)(x) が連続であるとする。
さらに f(n)(x) が a < x < b で n 回微分可能ならば
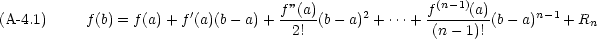
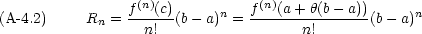
 < 1 であるような実数 c と
< 1 であるような実数 c と  とが存在する。この定理を Taylor の定理という。
とが存在する。この定理を Taylor の定理という。
Taylor の定理はつまり,関数 f(x) が x = a の付近(a b)で次のように「展開」出来るといっている。
b)で次のように「展開」出来るといっている。
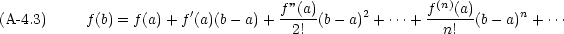
|b - a|が充分小さいとき,近似関数として Taylor 展開の最初の数項を使うことが出来る。
以下に頻繁に使用される関数の Maclaurin 展開を示す。