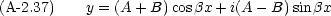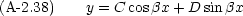A-2 初等微分方程式
プリントに登場する初歩的な微分方程式の解法について解説する。
A-2.1 y' = g(x)
まず手始めに,次の形の一階微分方程式を考える。
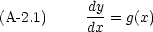
この方程式は直ちに積分できる。
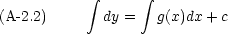
この積分は不定積分で, c は積分定数である。つまり
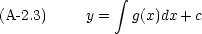
物理的な問題でこのような微分方程式を解く場合,定数 c は問題設定で与えられる条件に合うように選ばなければならない。
これは,以下にでてくる全ての積分定数について,同様である。
A-2.2 y' + ay = g(x)
もう少し進んだ形として,次の方程式を考える。
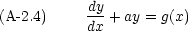
これを解くために次のような式を思い出す。
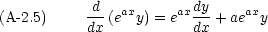
式 (A-2.4) の両辺に e
ax をかけ,式 (A-2.5) を用いると
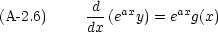
この方程式は直ちに積分できる。
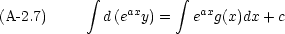
つまり
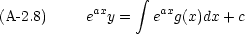
さらに書き換えると
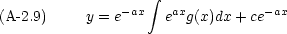
とくに, g(x) = 0 の場合には
A-2.3 y'' + ay' + by = 0
物理でよく登場するのが次の形の方程式である。
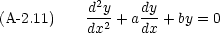
これを解くためには,まず次のような形に変形できるかどうかを考える。
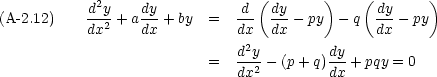
ここで p, q は定数である。この式から

が成り立たなければならないことがわかる。これは, p, q が次の二次方程式の二根であるということである。
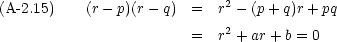
根の公式から
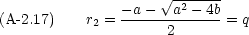
勿論 r
1 = q, r
2 = p としても以下の話には影響がない。ここで,式 (A-2.12) の方程式にもどる。
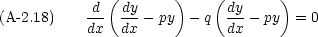
さらに次のような関数を定義する。
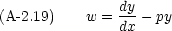
とすれば式 (A-2.18) は次のようになる。
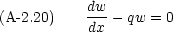
この形の微分方程式の解は式 (A-2.10) で既に述べた。

これを式 (A-2.19) に代入する。
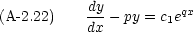
この形の微分方程式の解も既に式 (A-2.9) で述べた。
ここから先は p = q の場合と p 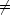 q の場合とで対応が異なる。
q の場合とで対応が異なる。
まず p = q の場合
次に, p 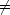 q の場合
q の場合
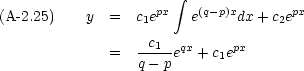
c
1, c
2 は任意なので,この式は次のように書いても同じ意味である。
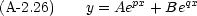
さて,一般に p, q は複素数なので, A, B も任意の複素数である。
式 (A-2.16) からわかるように, a2 - 4b > 0 の場合は p, q は異なる実数であり,式 (A-2.26) にそのまま当てはめて何の問題もない。
a2 - 4b = 0 の場合は p = q の実数なので式 (A-2.24) を用いる。
a2 - 4b < 0 の場合は p, q は共役複素数となるので補足説明がいる。 p, q を次のように書くことにする。
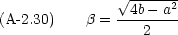
式 (A-2.26) は次のようになる。
このように,式 (A-2.11) の解は二つの任意定数を含んだ形でかける。
このような任意定数を含んだ解を一般解という。
任意定数が二つ必要なのは,式 (A-2.11) が二階の微分方程式だからである。
先にも述べたように,任意定数は,物理的な問題設定で与えられる条件に合うように選ばなければならない。
A-2.4 y''± β2y = 0
式 (A-2.11) で特に a = 0 の場合を考える。 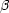 を実数として
を実数として
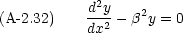
この場合
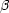 2
2 > 0 で, p =
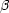
, q = -
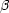
だから,式 (A-2.24) の形で解がかける。

次に
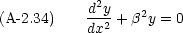
この場合 p = i
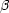
, q = -i
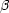
だから,式 (A-2.31)をつかえばよい。
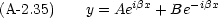
これは一般解の一つの表現方法だが,これで事足りたわけではない。これと全く同等で別の書き方が可能である。 Euler の公式を思い出す。
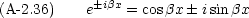
この式を式 (A-2.35) に代入すると
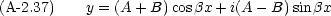
ここで A, B は任意の複素数だから次のように書いても意味は変わらない。
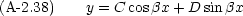
つまり,式 (A-2.34) の一般解には二つの表現法がある。
一つは式 (A-2.35) もう一つは式 (A-2.38) である。注意すべきことは,二つは同等だということである。
式 (A-2.35) で表される関数は C, D を適当に選べば必ず式 (A-2.38) で表現できる。
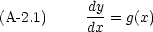
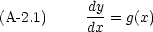
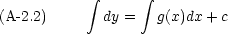
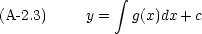
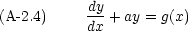
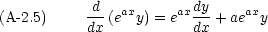
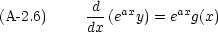
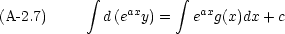
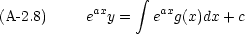
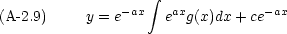

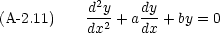
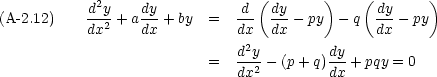
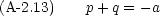

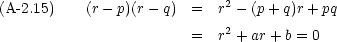
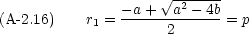
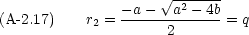
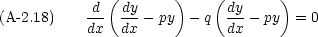
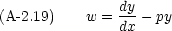
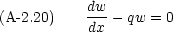 この形の微分方程式の解は式 (A-2.10) で既に述べた。
この形の微分方程式の解は式 (A-2.10) で既に述べた。 
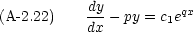
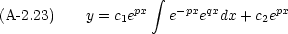
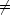 q の場合とで対応が異なる。
q の場合とで対応が異なる。
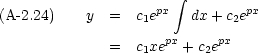
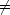 q の場合
q の場合
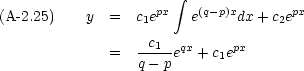
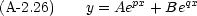
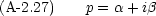


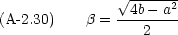 式 (A-2.26) は次のようになる。
式 (A-2.26) は次のようになる。
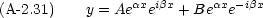
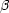 を実数として
を実数として
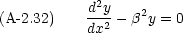
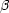 2 > 0 で, p =
2 > 0 で, p = 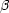 , q = -
, q = -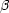 だから,式 (A-2.24) の形で解がかける。
だから,式 (A-2.24) の形で解がかける。

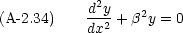
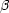 , q = -i
, q = -i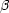 だから,式 (A-2.31)をつかえばよい。
だから,式 (A-2.31)をつかえばよい。