A-1 簡単な微積分の公式

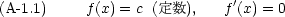
老婆心ながら，プリントに登場する初歩的な微積分の公式をまとめておく。

A-1.1 微分公式

まず，簡単な関数の微分公式をまとめる。微分はダッシュ記号で表すものとする。つまり df(x)/dx = f'(x) = f'である。

三角関数の引数は全てラジアンで表す。

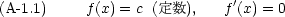
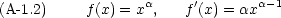
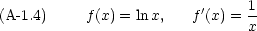
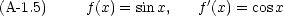
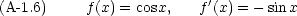
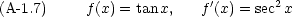
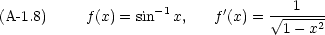
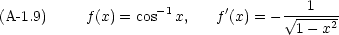
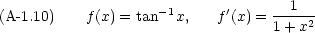
実際の計算には，次のような公式も必要になる。

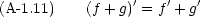
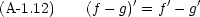
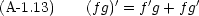
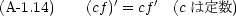
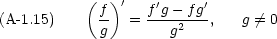
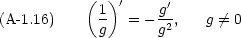
合成関数の微分も頻繁に必要になる。 y = f(z), z = g(x) である時

A-1.2 積分公式

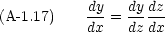
まず，簡単な関数の不定積分をまとめる。積分定数は省略する。

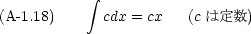
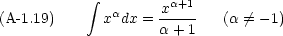
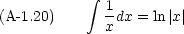
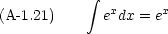
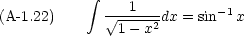
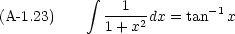
実際の計算には，次のような公式も必要になる。

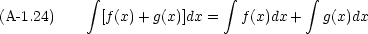
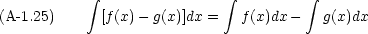
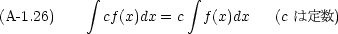
置換積分は日常的に用いる。 x = (t) とかけるとき

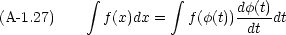
部分積分は頻繁に用いる。

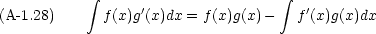
三角関数の積分がよくでてくる。

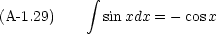
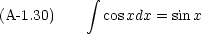
加法定理

特に x = y の場合

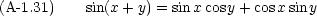
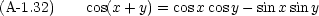
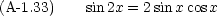
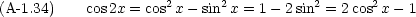
これを思い出すと次のような積分は簡単にわかる

最後の積分は置換積分でもできる。
t = cosx とすれば dt = -sinxdx だから

また s = sinx とすれば ds = cosxdx だから

ここでは積分定数を省略している，本来，不定積分には任意の積分定数を加える必要があるので，上の３式は同等である。

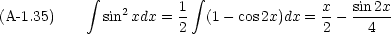
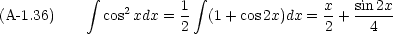
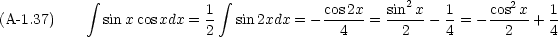
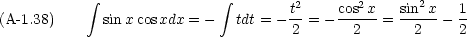
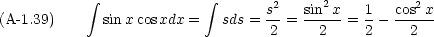
次のような形の積分も必要になる。

つまり f(x) = x, g'(x) = sin²x として部分積分を行った。

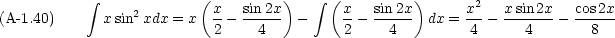
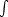x² sin²xdx のような積分も必要だが，これは上の要領で部分積分を繰り返せばよいので，演習問題とする。