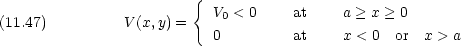11: トンネル効果
量子的な粒子は古典的に許されない領域でも存在確率がゼロではない場合がある。
これは古典的には越えられないようなポテンシャル障壁を粒子が越えていく可能性があることを示唆している。
このような現象はトンネル効果と呼ばれており,化学反応を考える上でも非常に重要である。
11.1 運動量と運動エネルギーの確定した粒子
11.1.1 粒子の密度

周期境界条件による規格化周期 L とすると
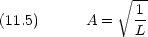
L あたり 1 個の粒子が存在する
|A|
2 が正方向に流れる粒子の密度を表す
運動量 p の粒子と-p の粒子がある場合
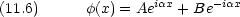
全粒子密度は

p の粒子の密度は|A|
2,-p の粒子の密度は|B|
2
11.1.2 粒子の流れの密度
粒子の流れの密度は,ある地点を単位時間に横切る粒子の数
数密度と速度との積で表される
p の粒子の流れの密度は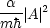 ,-p の粒子の流れの密度は
,-p の粒子の流れの密度は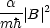
11.2 無限に厚い壁に衝突する粒子
11.2.1 古典論
質量 m の粒子が x = - から正の方向に等速で飛んでくるとする
から正の方向に等速で飛んでくるとする
E < V 0 のとき x = 0 でポテンシャルの壁に衝突する
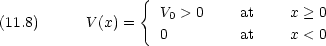
完全弾性衝突して,同じ運動エネルギーで負の方向に飛んでいく
粒子が x > 0 の領域に来ることはない
11.2.2 量子論
Schr dinger 方程式
dinger 方程式
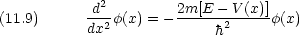
解は領域ごとに違う形で表される。
まず, x < 0 について
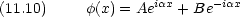
次に x > a について
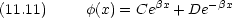
ここで
境界条件  (x) と
(x) と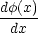 とが x = 0 で連続
とが x = 0 で連続
ただし C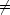 0 では波動関数が x
0 では波動関数が x 
 で発散するので C = 0
で発散するので C = 0
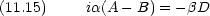
未知数 3 つで方程式 2 つなので全ての係数が決まるわけではない
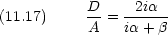
|A|
2 = |B|
2 である
|D|
2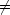
0 である

古典的に許されない部分でも波動関数がゼロでない
11.3 有限の厚さの壁に衝突する粒子
11.3.1 古典論
質量 m の粒子が x = - から正の方向に等速で飛んでくるとする
から正の方向に等速で飛んでくるとする
E < V 0 のとき x = 0 でポテンシャルの壁に衝突する
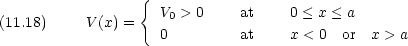
完全弾性衝突して,同じ運動エネルギーで負の方向に飛んでいく
壁の厚さに関わりなく粒子が x > 0 の領域に来ることはない
11.3.2 量子論
Schr dinger 方程式
dinger 方程式
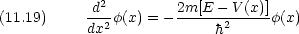
解は,領域ごとに形が異なる。
まず, x < 0
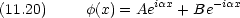
次に 0 < x < a
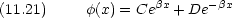
そして x > a
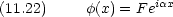
粒子はもともと x = -

から飛んできたと考えているので,
x > a の領域には負の運動量の粒子(つまりどこかで跳ね返った粒子)はあり得ない。よって Ge
-i x
x は考慮しない
境界条件

(x) と
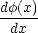
とが x = 0 及び x = -a で連続
まず x = 0 において
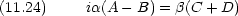
次に x = a
未知数 5 つで方程式 4 つなので全ての変数が決まるわけではないので, A に対する比を求める。
粒子の流れの密度
x < 0 で正方向について

負方向は

x > a については正方向のみで
反射率 R と透過率 T は流れの密度の比できまる
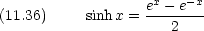
ポテンシャルの壁をすり抜けていく粒子がある
粒子は保存するので
11.4 有限の障壁の上を通る粒子
上と同じポテンシャルで E > V 0 の場合
古典的には,粒子はポテンシャルと無関係に等速で飛び去っていく(跳ね返る粒子はない)
量子的な波動関数は,領域ごとに次のように書ける。
x < 0 について
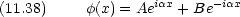
0 < x < a では
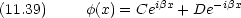
x > a では
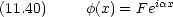
ただし
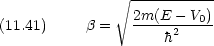
途中計算は省略するが
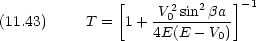
E > V
0 であるにも関わらず跳ね返る粒子がある
11.5 化学反応とトンネル効果
活性化エネルギーとポテンシャル障壁
軽い原子(水素)でトンネル効果が重要
低温ほどトンネル効果が重要
演習問題
-
波動関数が

で与えられる質量 m の粒子について,確率の流れの密度 j を一次元で次のように定義する。
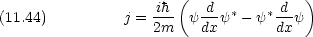
波動関数が次のように与えられるときの確率の流れの密度を計算せよ。
 = Aeikx
= Aeikx
 = Aeikx + Be-ikx
= Aeikx + Be-ikx
-
次のようなポテンシャル V (x) 上を質量 m の粒子が x = -

から正方向に一次元運動する。
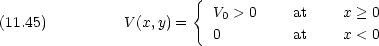
- 運動エネルギー E が V 0 > E > 0 の場合について,透過率と反射率を計算せよ。
- E > V 0 の場合について, (1) と同様の計算を行え。
- それぞれの場合について,透過率と反射率の和が 1 であることを示せ。
- (1), (2) の結果を古典論の予測と比較せよ。
-
次のようなポテンシャル V (x) 上を質量 m の粒子が x = -

から正方向に一次元運動する。
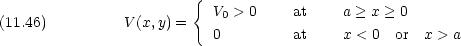
- 運動エネルギー E が V 0 > E > 0 の場合について,透過率と反射率を計算せよ。
- E > V 0 の場合について, (1) と同様の計算を行え。
- それぞれの場合について,透過率と反射率の和が 1 であることを示せ。
- (1), (2) の結果を古典論の予測と比較せよ。
-
次のようなポテンシャル V (x) 上を質量 m の粒子が x = -

から正方向に一次元運動する。
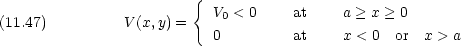
- 運動エネルギー E が E > 0 の場合について,透過率と反射率を計算せよ。
- 透過率と反射率の和が 1 であることを示せ。
- (2) の結果を古典論の予測と比較せよ。
- 粒子の運動エネルギーがポテンシャルの障壁より小さいとき次の問に答えよ。
- ポテンシャル障壁が高い場合と低い場合でどちらがトンネル現象を起こしやすいか。
- ポテンシャル障壁が厚い場合と薄い場合でどちらがトンネル現象を起こしやすいか。
- 粒子の質量が重い場合と軽い場合でどちらがトンネル現象を起こしやすいか。
- 化学反応速度について。
- Arrhenius プロットとはどのようなプロットか。
- 速度定数に対する Arrhenius の式とはどのような式か。
- トンネル効果が重要である場合, Arrhenius プロットは直線からどのようにずれるか。

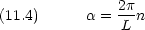
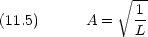
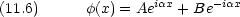

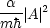 ,-p の粒子の流れの密度は
,-p の粒子の流れの密度は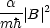
 から正の方向に等速で飛んでくるとする
から正の方向に等速で飛んでくるとする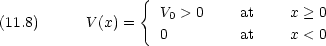
 dinger 方程式
dinger 方程式
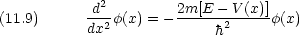
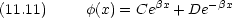
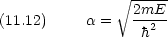
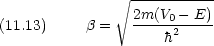
 (x) と
(x) と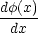 とが x = 0 で連続
とが x = 0 で連続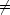 0 では波動関数が x
0 では波動関数が x 
 で発散するので C = 0
で発散するので C = 0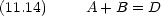
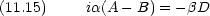
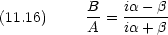
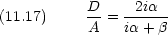
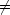 0 である
0 である 古典的に許されない部分でも波動関数がゼロでない
古典的に許されない部分でも波動関数がゼロでない
 から正の方向に等速で飛んでくるとする
から正の方向に等速で飛んでくるとする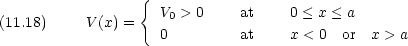
 dinger 方程式
dinger 方程式
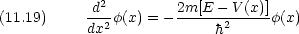
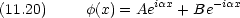
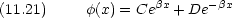
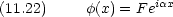
 から飛んできたと考えているので,
から飛んできたと考えているので, x は考慮しない
x は考慮しない  (x) と
(x) と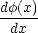 とが x = 0 及び x = -a で連続
とが x = 0 及び x = -a で連続 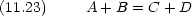
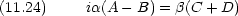
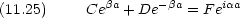
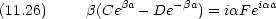
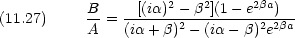
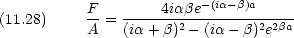
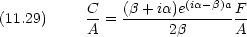
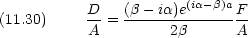


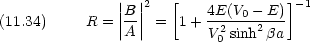
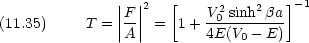

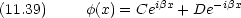
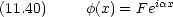
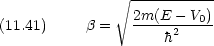
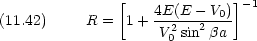
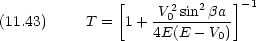
 で与えられる質量 m の粒子について,確率の流れの密度 j を一次元で次のように定義する。
で与えられる質量 m の粒子について,確率の流れの密度 j を一次元で次のように定義する。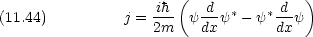
 = Aeikx
= Aeikx
 = Aeikx + Be-ikx
= Aeikx + Be-ikx
 から正方向に一次元運動する。
から正方向に一次元運動する。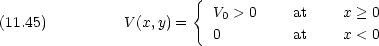
 から正方向に一次元運動する。
から正方向に一次元運動する。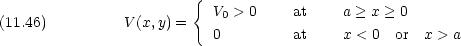
 から正方向に一次元運動する。
から正方向に一次元運動する。