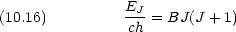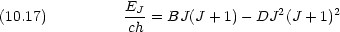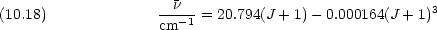10: 二原子分子の回転振動スペクトル
10.1 分光学
10.1.1 Lambert-Beer の法則
Lambert の法則
光を吸収する媒体がある。 dx の厚さの媒体を透過すると,光の強度 I が dI だけ減少する
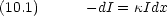
厚さ l の媒体について積分形で書くと

普通は吸光度 A を次のように定義する
Beer の法則
濃度 c と光吸収の関係
Lambert-Beer の法則
Lambert と Beer とを組み合わせると
10.1.2 吸収強度を決めるもの
量子力学的な状態 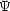 n から
n から 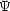 m への,光吸収による遷移について
m への,光吸収による遷移について
Bohr の条件
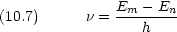
遷移モーメント
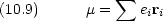
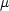
は双極子モーメント(ベクトル)で,分子中の電気的な偏りを表す
10.1.3 赤外吸収
振動により双極子モーメントが変化する場合吸収が起こる
等核二原子分子は赤外不活性
調和振動近似 異核二原子分子で
異核二原子分子で 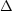 v = ±1 の場合のみ振動による赤外吸収あり
v = ±1 の場合のみ振動による赤外吸収あり
v は振動の量子数(前節では n)
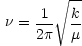 に対応する光が吸収される
に対応する光が吸収される
ただし,振動のスペクトルには回転のスペクトルが重なるのでそんなに単純ではない
多原子分子の場合 基準振動解析をして調和振動子の重ね合わせに近似する
基準振動解析をして調和振動子の重ね合わせに近似する
10.1.4 Raman 散乱
分子に振動数  0 の可視光をあて散乱を観測する
0 の可視光をあて散乱を観測する
Rayleigh 散乱  0
0
Raman 散乱  0 ±
0 ± 
 が赤外吸収の
が赤外吸収の  に対応
に対応
分極率の変化を伴う振動が Raman 活性(等核二原子分子の振動がみえる)
選択率 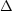 v = ±1
v = ±1
赤外吸収と Raman 散乱は相補的
10.2 分子の回転スペクトル
振動の場合と同様,回転運動も光の吸収スペクトルから観測することができる。吸収する光の波長は振動の場合よりもずいぶん長い。
10.2.1 選 択 律
| Bohr の条件 |
 = = 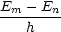 |
| 遷移モーメント |
Rmn = <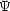 m| m|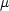 | |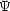 n> n> |
10.2.2 赤外吸収
回転運動による双極子モーメントの変化が重要
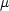
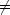 0 で,
0 で, 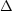 J = ±1,かつ
J = ±1,かつ 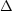 m = 0,±1 のときのみ R
m = 0,±1 のときのみ R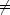 0
0
異核二原子分子は回転に関して赤外活性
等核二原子分子の回転は,赤外吸収スペクトルでは見えない
10.2.3 Raman 散乱
回転による分極率の変化が重要
等核二原子分子も活性 ただし線形分子に対して
ただし線形分子に対して 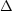 J = ±2
J = ±2
10.2.4 多原子分子の回転
線形分子の場合, I が一つ→二原子分子と同じ
一般に I は 3 つ→話は複雑
10.3 振動回転スペクトル
二原子分子では一般に振動準位の遷移は回転準位の遷移を伴って起きる。
よって,純粋に振動のみのスペクトルを観測することはできない。
演習問題
- 波長 440 nm で,厚さ 2 mm のガラスフィルターの透過率は 81.0 % である。
- 吸光度はいくらか。
- 厚さ 8 mmのフィルターでは透過率はいくらか。
- 波長 540 nm で MnO4- イオンのモル吸光係数は 202.5 m2 mol-1 である。
20.000 g の合金を溶解し,溶液中 のマンガンを酸化して MnO4- とする。その溶液をメスフラスコで 500.0 ml に希釈した後,
540 nm における透過率を 1.00 cm セルで測定したところ, 32.5 % であった。合金中のマンガンの含量を重量 % で計算せよ。
- モル質量 425 g mol-1 の染料 0.100g を 100ml のアルコールに溶解させた。
この溶液 1.00 ml を 250.0 ml に希釈し 1.00 cmセルで透過率を測定したところ, 55.0 %であった。
- 染料のモル吸光係数はいくらか。
- 透過率の測定を原液で行わなかったのは何故か。
- 熱運動のエネルギーは kBT 程度であると考えられる。次の波長
 の光の光量子のエネルギーはどの程度の温度に相当するか。
の光の光量子のエネルギーはどの程度の温度に相当するか。
 = 250 nm の紫外線
= 250 nm の紫外線
 = 500 nm の可視光線
= 500 nm の可視光線
 = 1 mm の近赤外線
= 1 mm の近赤外線
 = 100 mm の遠赤外線
= 100 mm の遠赤外線
 = 10 mm のマイクロ波
= 10 mm のマイクロ波
-
ハロゲン化水素の基本振動

は次の通りである。
| |
1H17F |
1H35Cl |
1H81Br |
1H127I |
 /cm-1 /cm-1 |
4141.3 |
2988.9 |
2649.7 |
2309.5 |
- 換算質量を求めよ。
- 力の定数を求めよ。
- 振動が古典的であるとしたときの周期を求めよ。
- これら分子の振動は,赤外活性か。また, Raman 活性か。
- 同位体置換で力の定数が変化しないとしたとき,1H を2D で置換したときの基本振動を求めよ。
-
ハロゲン分子の力の定数 k は次のとおりである。
| |
17F 2 |
35Cl 2 |
79Br 2 |
| k/N m-1 |
445 |
322 |
240 |
- 基本振動の波数を求めよ。
- ゼロ点エネルギーを求めよ。
- これら分子の振動は,赤外活性か。また, Raman 活性か。
-
次の 2 原子分子の基本振動

から原子間距離の標準偏差を求め,平衡核間距離 R と比較せよ。
| |
1H2 |
14N2 |
16O2 |
32S2 |
 /cm-1 /cm-1 |
4330 |
2350 |
1580 |
726 |
| R/nm |
0.074 |
0.110 |
0.121 |
0.189 |
-
化学結合した 2 つの原子の間のポテンシャルを近似的に表す関数として Morse 関数がある。
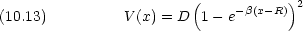
ここで D,
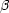
, R は定数である。
- 極小の座標,深さを求めよ。
- 極小付近を調和振動子近似した場合の基本振動の波数
 を求めよ。
を求めよ。
- Morse ポテンシャルに対するエネルギー準位を波数単位で表すと次のようになることが知られてい る。
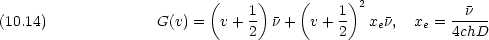
xe は非調和定数と呼ばれている。 v は振動の量子数である。
次の H35Cl 分子の振動バンド中心波数のデータからゼロ点エネルギーと解離エネルギーを見積もれ。
| 振動量子数 |
0→1 |
0→2 |
0→3 |
0→4 |
0→5 |
| バンド中心/cm-1 |
2885.98 |
5667.98 |
8346.78 |
10992.81 |
13396.19 |
- ベンゼンの基本振動のうち Raman 活性なものが, 3062 cm-1 と 992 cm-1 にある。
波長 488.0 nm の Ar-Kr レーザーを用いた場合,ベンゼンの振動 Raman バンドの中心はどの波長に観測されるか。
-
次の基本振動数のデータが与えられている。
| 分子 |
1H35Cl |
2D35Cl |
1H2D |
2D 2 |
| 基本振動数/cm-1 |
2989 |
2144 |
3817 |
2990 |
次の反応の
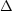
H
o を計算せよ。
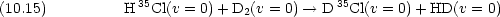
-
Born-Oppenheimer 近似では, 2 原子分子の電子エネルギーは核間距離のみに依存する。
次の基本振動数のデータが与えられている。このことを用いて H
2 と D
2 の振動準位の違いについて説明せよ。
| |
1H 2 |
2D 2 |
 /cm-1 /cm-1 |
4330 |
2990 |
- 剛体 2 原子分子の純回転スペクトルは等間隔に並んだピークの列になることを示せ。
-
剛体回転のエネルギー準位は回転定数 B を用いて表されることが多い。
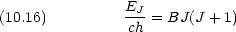
B は通常 cm
-1 単位で表す。
- 回転定数を物理定数と慣性モーメントで表せ。
- 2 原子分子の赤外吸収スペクトルのピーク間隔を B を用いて表せ。
-
次の各分子の回転定数から平衡核間距離を見積もれ。
| 分子 |
H2 |
14C2 |
16O2 |
35Cl2 |
| B/cm-1 |
60.80 |
2.010 |
1.446 |
0.244 |
| 分子 |
H35Cl |
H79Br |
12C16O |
14N16O |
| B/cm-1 |
10.591 |
8.473 |
1.931 |
1.705 |
- J が大きいときには,回転遷移を起こす電磁波の周波数が,始状態ないしは終状態における分子の古典的周波数に近似的に等しいことを示せ。
-
実際の 2 原子分子の回転エネルギー準位は次のような形の式で近似できる。
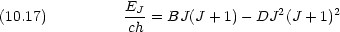
- 右辺第 2 項は何に起因する項と考えられるか。
- H35Cl の純回転スペクトルのピーク位置は次の式で表されることが実験的に知られている。
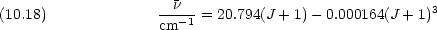
D を見積もれ。
- 線形 3 原子分子について。
- 重心は, 3 つの原子の質量と 2 つの平衡核間距離とを用いてどのように表されるか。
- 分子軸に垂直で重心を通る軸の周りの慣性モーメントはどうなるか。
- CO2 の C=O 結合距離(0.116 nm)から回転スペクトル間隔を見積もれ。
- 2 原子分子気体の近赤外吸収スペクトルに於ける P 枝, Q 枝, R 枝について解説せよ。
- 2 原子分子気体の Raman 散乱スペクトルに於ける O 枝, Q 枝, S 枝について解説せよ。
- 12C14N の平衡核間距離は 0.117 nm, 力の定数は 1630 N m-1 である。
どのような振動回転スペクトルを与えるか。赤外吸収, Raman 散乱の両方についてのべよ。
- 1H35Cl の平衡核間距離は 0.1287 nm, 基本振動数は 2990.95 cm-1 である。
- 回転振動スペクトルの形状を予測せよ。
- 力の定数が変化しないとして,1H37Cl, 2D35Cl, 2D37Cl の回転振動スペクトルの形状を予測せよ。
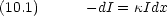
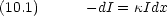
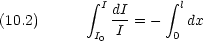

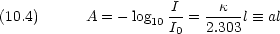


 n から
n から  m への,光吸収による遷移について
m への,光吸収による遷移について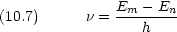
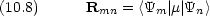
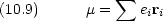
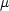 は双極子モーメント(ベクトル)で,分子中の電気的な偏りを表す
は双極子モーメント(ベクトル)で,分子中の電気的な偏りを表す
 異核二原子分子で
異核二原子分子で 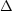 v = ±1 の場合のみ振動による赤外吸収あり
v = ±1 の場合のみ振動による赤外吸収あり 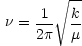 に対応する光が吸収される
に対応する光が吸収される  基準振動解析をして調和振動子の重ね合わせに近似する
基準振動解析をして調和振動子の重ね合わせに近似する
 0 の可視光をあて散乱を観測する
0 の可視光をあて散乱を観測する  0
0  0 ±
0 ± 
 が赤外吸収の
が赤外吸収の  に対応
に対応 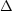 v = ±1
v = ±1  =
= 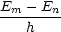
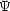 m|
m|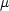 |
|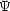 n>
n>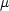
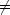 0 で,
0 で, 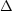 J = ±1,かつ
J = ±1,かつ 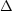 m = 0,±1 のときのみ R
m = 0,±1 のときのみ R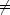 0
0 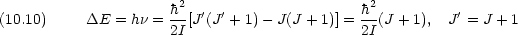
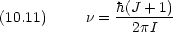
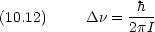
 ただし線形分子に対して
ただし線形分子に対して 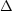 J = ±2
J = ±2
 の光の光量子のエネルギーはどの程度の温度に相当するか。
の光の光量子のエネルギーはどの程度の温度に相当するか。
 = 250 nm の紫外線
= 250 nm の紫外線
 = 500 nm の可視光線
= 500 nm の可視光線
 = 1 mm の近赤外線
= 1 mm の近赤外線
 = 100 mm の遠赤外線
= 100 mm の遠赤外線
 = 10 mm のマイクロ波
= 10 mm のマイクロ波
 は次の通りである。
は次の通りである。  /cm-1
/cm-1 から原子間距離の標準偏差を求め,平衡核間距離 R と比較せよ。
から原子間距離の標準偏差を求め,平衡核間距離 R と比較せよ。  /cm-1
/cm-1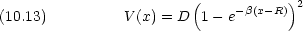
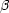 , R は定数である。
, R は定数である。
 を求めよ。
を求めよ。
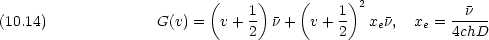
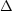 Ho を計算せよ。
Ho を計算せよ。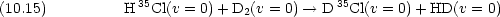
 /cm-1
/cm-1