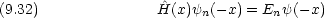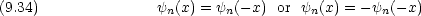9: 一次元調和振動子
物体が振動している状態を表す最も簡単なモデルが調和振動子モデルである。
化学においては分子の振動を解析する際に重要なモデルである。この節では,量子的な理論を解説する。
9.1 Schr dinger 方程式
dinger 方程式
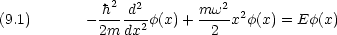
変数変換する
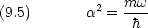
境界条件は波動関数が一価・有界・連続・一回微分連続であることと
9.2 |x|→∞ における漸近解
いきなり解くことはできないので, |x|
 のときの近似解を求める。方程式は次のようになる
のときの近似解を求める。方程式は次のようになる
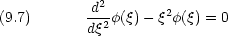
一般解

境界条件から A = 0
9.3 一般の場合
方程式の解が次の形に書けると仮定する ( N は規格化定数 )
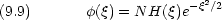
微分して見る
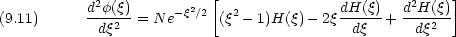
Schr

dinger 方程式に代入して整理する
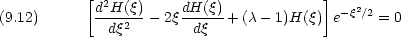
上の方程式を常に満足するには […] の中がゼロでなければならない
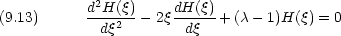
これが解くべき方程式である(Hermite 方程式)。この解は次の式で与えられる。
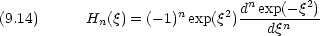
H
n は n 次の多項式(Hermite 多項式という)で, n が奇数の場合は奇関数, n が偶数の場合は偶関数である。
9.4 波動関数
規格化定数 N として
はじめのいくつかについて, Hermite 多項式を具体的に書き下す
9.5 エネルギー準位
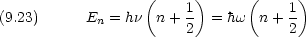
基底状態のエネルギーはゼロではない(ゼロ点エネルギー・ゼロ点振動)
演習問題
- 一次元調和振動子について。
- n = 0 〜 2 の場合の規格化された波動関数を具体的に書き下せ。
- 前問の波動関数が互いに直交していることを示せ。
- 一次元調和振動子について。
- n = 0 と n = 1 の場合について粒子の存在確率密度を位置の関数として表せ。
- 前問の結果を古典論と比較せよ。
- 量子数が大きくなった場合の粒子の存在確率の分布密度を模式的に描け。
- 前問の結果を古典論と比較せよ。
- 一次元調和振動子の n = 0 と n = 1 の場合について,古典的に許されない位置で粒子を観測する確率を求めよ。
- Hermite の性質を利用して,一次元調和振動子について以下の問いに答えよ。
- 各準位の規格化された波動関数を書け。
- 異なる準位の波動関数の直交性を確認せよ。
- 位置の期待値および分散を量子数の関数として計算せよ。
- 運動量の期待値と分散とを量子数の関数として計算せよ。
- 位置と運動量の不確定性がそれぞれの分散の平方根で与えられるとして,不確定性原理が満たされているかどうかを確かめよ。
- (3), (4) の結果を古典論と比較せよ。
- 運動エネルギーの期待値<T>と位置エネルギーの期待値<V >を量子数の関数として計算せよ。
- 一次元でポテンシャルエネルギーが xn に比例するとき, 2<T> = n<V >の関係が成り立つことが知られている。
これを量子的ヴィリアル定理という。前問の結果がこの関係を満たすことを示せ。
-
遷移モーメント R
mn を次のように定義する。
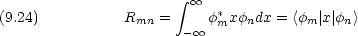
この量がゼロにならないのは m と n がどんな値になるときか。エルミート多項式の性質を利用して,一次元調和振動子について計算せよ。
-
一次元調和振動子の波動関数
 n
n に次のような演算子を作用させるとどのような関数になるか。
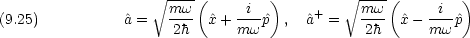
前者を下降演算子,後者を上昇演算子という。
-
質量 m の粒子のポテンシャル V (x) 中における運動を量子力学的に考察する。ただし k は定数である。
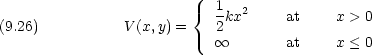
- Schr
 dinger 方程式を書き下せ。
dinger 方程式を書き下せ。
- 波動関数に対する境界条件はどうなるか。
- エネルギー準位と規格化された波動関数を求めよ。
-
-
-
- ポテンシャル
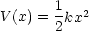 中に於ける質量 m の粒子の一次元運動について考える。
中に於ける質量 m の粒子の一次元運動について考える。
-
ハミルトニアンが x を-x と置き換えるような操作について対称であることを示せ。

-
前問の結果から Schr

dinger 方程式が次のように書けることを示せ。
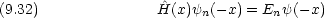
-
縮退のない場合 c を定数として次の関係が成り立たなくてはならない。

前問の結果から波動関数は x = 0 について対称又は反対称であることを示せ。
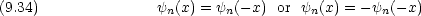
 dinger 方程式
dinger 方程式  dinger 方程式
dinger 方程式 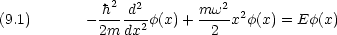
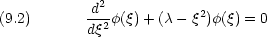


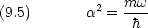
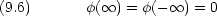

 のときの近似解を求める。方程式は次のようになる
のときの近似解を求める。方程式は次のようになる
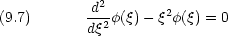

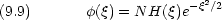
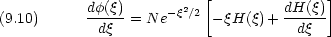
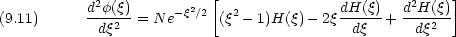
 dinger 方程式に代入して整理する
dinger 方程式に代入して整理する
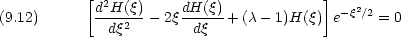
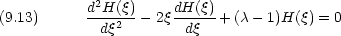
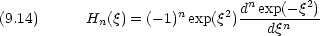
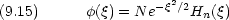
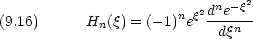
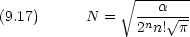

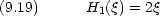
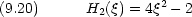
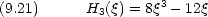
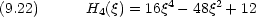
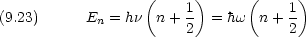
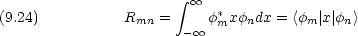
 n に次のような演算子を作用させるとどのような関数になるか。
n に次のような演算子を作用させるとどのような関数になるか。 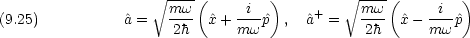
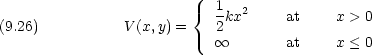
 dinger 方程式を書き下せ。
dinger 方程式を書き下せ。
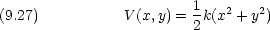
 dinger 方程式を書き下せ。
dinger 方程式を書き下せ。
 dinger 方程式がデカルト座標で変数分離出来ることを示せ。
dinger 方程式がデカルト座標で変数分離出来ることを示せ。
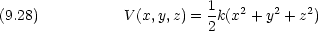
 dinger 方程式を書き下せ。
dinger 方程式を書き下せ。
 dinger 方程式がデカルト座標で変数分離出来ることを示せ。
dinger 方程式がデカルト座標で変数分離出来ることを示せ。
 は定数である。
は定数である。 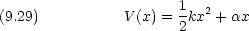
 dinger 方程式を書き下せ。
dinger 方程式を書き下せ。

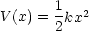 中に於ける質量 m の粒子の一次元運動について考える。
中に於ける質量 m の粒子の一次元運動について考える。

 dinger 方程式が次のように書けることを示せ。
dinger 方程式が次のように書けることを示せ。