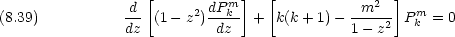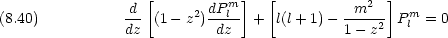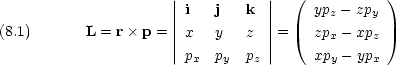
剛体の重心の周りの回転を量子力学的に考察する。
前節で見たように,古典的な角運動量は次のように書ける。
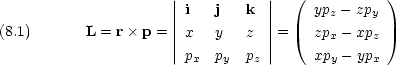
これの類推から,量子力学的な角運動量の演算子は次のようになるはずである。
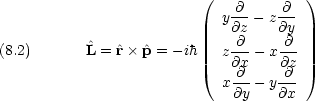
角運動量の 2 乗については
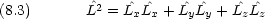
この演算子は,極座標を用いて書き直すことができる。
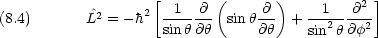
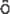 dinger 方程式
dinger 方程式 古典的に,回転運動のエネルギー Er が
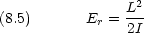
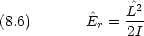
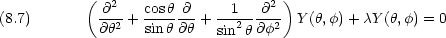
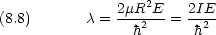
 dinger 方程式を極座標で表 し,動径部分と角度部分を変数分離した場合の角度部分の方程式に他ならない。
dinger 方程式を極座標で表 し,動径部分と角度部分を変数分離した場合の角度部分の方程式に他ならない。
ここでさらに波動関数が変数分離できるとする
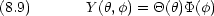
 ,
, ) で割り,
) で割り,  の部分と
の部分と  の部分に分ける
の部分に分ける 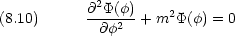
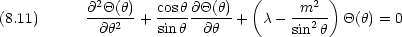
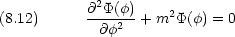
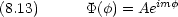
 は角度変数なので
は角度変数なので 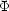 は周期 2
は周期 2 の周期境界条件を満たさなければならない
の周期境界条件を満たさなければならない
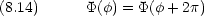
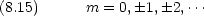
m を磁気量子数という
規格化定数 A は
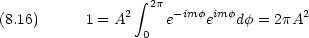
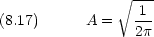
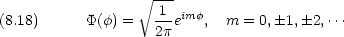
N を規格化定数として,  (
( ) = NP(
) = NP( ) と置くことにする
) と置くことにする
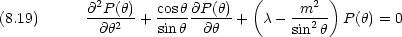
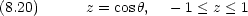
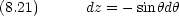
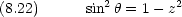
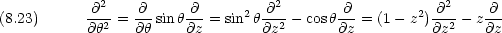
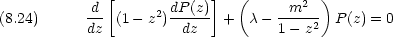
この方程式の解は  = l(l + 1) ただし l = 0,1,2,
= l(l + 1) ただし l = 0,1,2, として次のようになる。(Legendre 多項式)
として次のようになる。(Legendre 多項式)
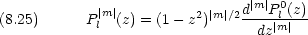
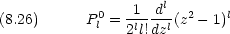
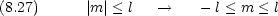
規格化定数 N は次のように決める
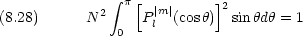
規格化された波動関数
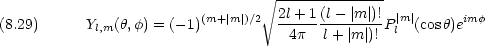

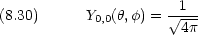
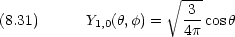
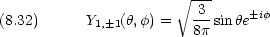
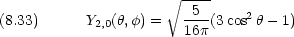
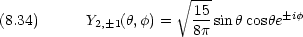
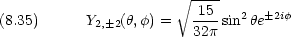
回転エネルギーは,量子数 l だけで決まる。通常は l のかわりに J (回転量子数)で表す
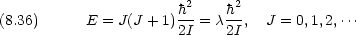
量子数 m は何を表しているのか。
m は角運動量の z 成分に比例する。これは,回転軸が任意の方向をとれるわけではないことを表している。
ただし,角運動量の z が確定した値を持てば, x, y 成分は不確定性原理によって,確定した値を持たない。
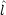 x,
x, 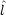 y,
y, 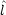 z をデカルト座標で表せ。
z をデカルト座標で表せ。

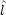 x,
x, 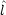 y,
y, 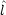 z の考えうる組み合わせについて交換子を求めよ。
z の考えうる組み合わせについて交換子を求めよ。
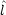 2 をデカルト座標で表せ。
2 をデカルト座標で表せ。
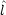 2 と
2 と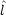 x,
x, 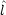 y,
y, 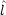 z と交換子を求めよ。
z と交換子を求めよ。
 ,
, ) は角運動量の z 成分の演算子の固有関数である。固有値は何か。
) は角運動量の z 成分の演算子の固有関数である。固有値は何か。
 ,
, ) は角運動量の 2 乗の演算子の固有関数である。固有値は何か。
) は角運動量の 2 乗の演算子の固有関数である。固有値は何か。
 dinger 方程式を極座標で変数分離したときの,
dinger 方程式を極座標で変数分離したときの, 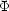 (
( ) に対する方程式について。
) に対する方程式について。

 dinger 方程式を満足することを示せ。
dinger 方程式を満足することを示せ。
 ,
, ) において,角運動量ベクトルが z 軸となす角度を求めよ。
) において,角運動量ベクトルが z 軸となす角度を求めよ。