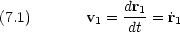
箱の中の粒子の問題は,いって見れば単原子分子の運動を取り扱っているが,
一般の多原子分子には分子内の運動があるため,さらに問題が複雑になる。
これ以降,多原子分子の最も簡単な例 として,二原子分子の運動を考えて行くが,
ここでは量子力学的な考察のための準備として,まず古典的に問題を解析する。
空間中に 2つの粒子があるとする。今のところ, 2 つの粒子が結合しているかどうかは問題にしない。質量は m1, m2 で位置は r1, r2 であるとする。
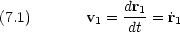
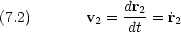


重心(質量中心)の座標
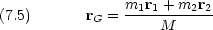
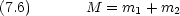
粒子 1 と 2 とは互いに相互作用を及ぼしあうが,外からの力はかかっていないものとする。
相互作用のポテンシャル V (r) は, 2つの粒子の距離 r のみで決まるとする。
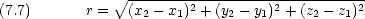
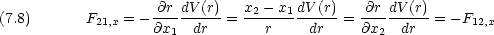
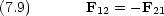
それぞれの粒子について運動方程式を書くと
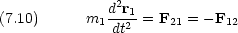
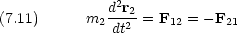
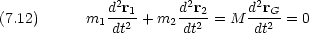
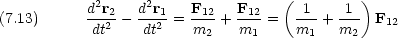
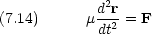


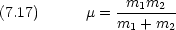
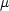 を換算質量という。
を換算質量という。
上の式は, 2 つの粒子の運動が,重心の(全体としての)運動と2粒子の相対的な運動の2つに分けて考えることができることを意味している。
その場合に,相対運動は,ポテンシャル V (r) 中を質量 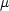 の粒子が 1 つ運動する場合と同じと見なして差し支えない。
の粒子が 1 つ運動する場合と同じと見なして差し支えない。
ちなみに,全エネルギーも重心運動部分と相対運動部分に分けられる。(ドットは時間に関する微分を表す記号である。)
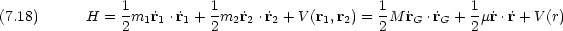
質点の運動の状態を表現するには vx, vy, vz の 3 つの変数を指定する必要がある。これを運動の自由度が3であるという。
質点が二つある場合,全自由度は 3×2 = 6 である。
二つの質点が二原子分子を構成する場合,自由度のうちわけは次のようになる
| 分子全体の並進の自由度 | 3 |
| 分子全体の回転の自由度 | 2 |
| 分子内振動の自由度 | 1 |
分子全体の並進は,先に述べた重心の運動に相当し,分子全体の回転と分子内振動とは相対運動に相当する。
そして,回転と振動とは近似的に独立に取り扱うことができる。
二原子分子の重心周りの回転を考える前に,まず,平面内の円軌道を巡る粒子について,
z 軸周りの回転を円柱座標で考える。粒子の質量は m で,軌道の半径 R は固定されているとする。
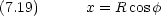
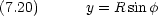
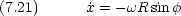
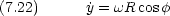

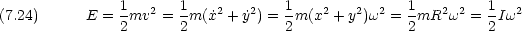

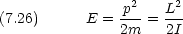

 に共役な力学変数 は L である。
に共役な力学変数 は L である。
ところで,「てこ」を考えたとき,支点からの距離に力点にはたらく力を掛けたものを「力のモーメント」という。
同様にして,「運動量のモーメント」というものも考えることができる。
力のモーメントと同様に運動量のモーメントは実はベクトルで,支点と力点を結ぶ線と運動量ベクトルを含む平面に垂直で右ねじの方向を向いているとする。
すると, z 方向のモーメントは xpy と ypx とで表されるが,
この二つではベクトルの方向が逆であることを考えると,合成するには引き算をしなければならない。
そうすると,角運動量とは運動量のモーメントに他ならないことが解る。
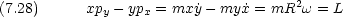
従って,この考え方を 3 次元に拡張すると次のようになる。
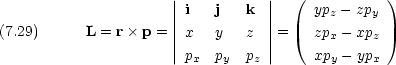
二原子分子に限らず,質点の相互位置が固定されている剛体を考える。重心の座標 rG は
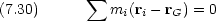
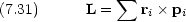
重心の周りの回転を考えるとき,慣性主軸というものを考えることができる。
x, y, z の各方向が慣性主軸の方向と一致するとき,回転運動のエネルギーは
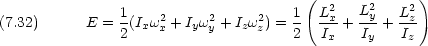

二原子分子では結合の方向を x 軸とすれば Ix = 0, Iy = Iz = R2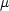 となる。 (R は平衡核間距離,
となる。 (R は平衡核間距離, 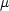 は換算質量)
は換算質量)
よって,二原子分子の回転は,質量 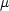 ,軌道半径 R の 1 粒子の円軌道運動に置き換えられる。
,軌道半径 R の 1 粒子の円軌道運動に置き換えられる。
古典的に考えた場合,この運動はある平面内での円運動になる。
分子の振動を考えるための準備に,単振動を考える。次のような円運動を一次元に投影した運動を単振動という。
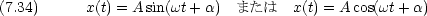
ここで, A は振幅,  は角振動数,
は角振動数,  は初期位相(t = 0 における位相), T = 2
は初期位相(t = 0 における位相), T = 2 /
/ は周期,
は周期,  = 1/T は振動数で ある。
= 1/T は振動数で ある。
 は円運動の角速度と等しい。この式は,次のような運動方程式の解である。
は円運動の角速度と等しい。この式は,次のような運動方程式の解である。
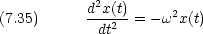
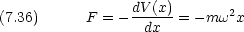
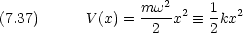
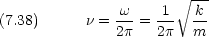
粒子のエネルギー E は保存するので,速度 v は座標のみできまる
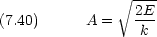
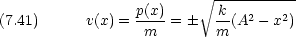
粒子を x 〜x + dx の範囲に見いだす確率 P(x)dx は, 1 周期の中でその部分に滞在する時間から計算できる。
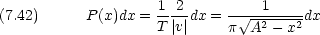
次のような仮定を置く
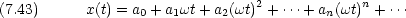
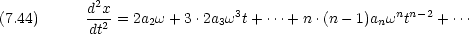
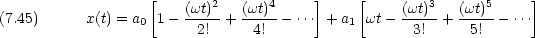
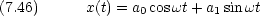
二原子分子では,原子の相対運動のみを考えた場合,核間距離 r の変化が振動である。
そして,先の考察によれば,これはポテンシャル 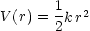 中の質量
中の質量 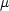 の粒子の一次元運動と同等である。よって振動数
の粒子の一次元運動と同等である。よって振動数  は
は
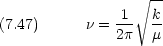
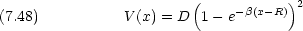
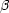 , R は定数である。
, R は定数である。
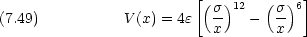
 ,
,  は定数である。
は定数である。
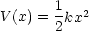 中を運動する。ただし k は定数である。
中を運動する。ただし k は定数である。
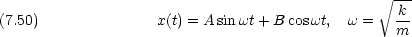
 は定数である。
は定数である。 
 を (2) の A, B を用いて表せ。
2 つの式は同じ関数の別の表現である。
を (2) の A, B を用いて表せ。
2 つの式は同じ関数の別の表現である。