 dinger 方程式の解法の典型的な例であるが,
dinger 方程式の解法の典型的な例であるが,実際の箱の中の粒子の問題に当てはめるためには,問題を三次元空間に拡張する必要がある。
このモデルは,理想気体の性質の計算に利用されている。
一次元の箱の中の粒子の問題は, Schr dinger 方程式の解法の典型的な例であるが,
dinger 方程式の解法の典型的な例であるが,
実際の箱の中の粒子の問題に当てはめるためには,問題を三次元空間に拡張する必要がある。
このモデルは,理想気体の性質の計算に利用されている。
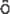 dinger 方程式 〜デカルト座標〜
dinger 方程式 〜デカルト座標〜
質量 m の粒子が三次元ポテンシャル V (x,y,z) 中を運動する場合の Schr dinger方程式
dinger方程式
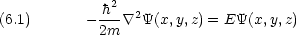
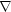 はナブラといいデカルト座標では次のようなベクトル演算子である
はナブラといいデカルト座標では次のようなベクトル演算子である
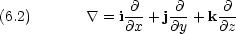
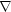 2 はラプラシアンといい,
2 はラプラシアンといい,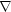 を 2 回はたらかせたもので,デカルト座標では
を 2 回はたらかせたもので,デカルト座標では
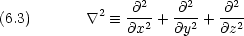
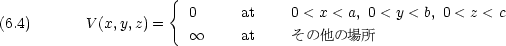
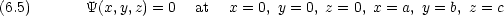
変数分離で方程式を解くことができる。
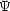 (x,y,z) = X(x)Y (y)Z(z) とおけると仮定する。
(x,y,z) = X(x)Y (y)Z(z) とおけると仮定する。
Schr dinger 方程式に代入 して両辺を
dinger 方程式に代入 して両辺を 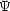 (x,y,z) = X(x)Y (y)Z(z) で割って整理すると
(x,y,z) = X(x)Y (y)Z(z) で割って整理すると
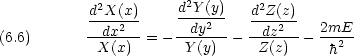
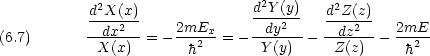
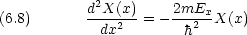
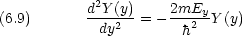
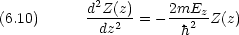
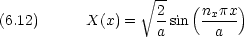
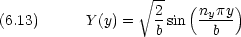
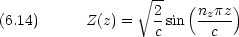
エネルギー準位は
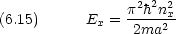
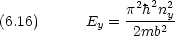
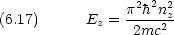
規格化条件
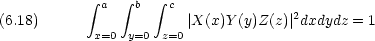
 という記号を使うこともある。この場合 d
という記号を使うこともある。この場合 d = dxdydz であり
= dxdydz であり
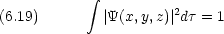
トータルの波動関数
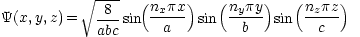
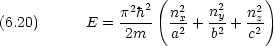
立方体の場合 a = b = c
N = nx2 + ny2 + nz2 = 6 の状態は (1,1,2), (1,2,1), (2,1,1) の 3 種類ある 3 重縮退
3 重縮退
立方体の中の粒子の縮態度 
| N |  |
N | 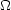 |
| 3 | 1 | 14 | 6 |
| 6 | 3 | 17 | 3 |
| 9 | 3 | 18 | 3 |
| 11 | 3 | 19 | 3 |
| 12 | 1 | 21 | 6 |
 dinger 方程式 〜極座標〜
dinger 方程式 〜極座標〜問題によっては,デカルト座標以外の座標系を用いる方が便利なこともある。例えば,ポテンシャルが球対称である場合には極座標がよく使われる。
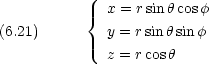
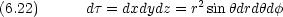
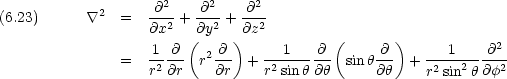
Schr dinger 方程式の極座標表示
dinger 方程式の極座標表示
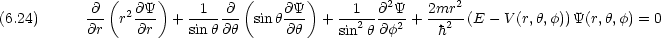
もしもポテンシャルが原点からの距離 r = 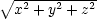 (動径)のみで決まるとすれば,
(動径)のみで決まるとすれば,
Schr dinger 方程式は,角度部分と動径部分に変数分離できる。
dinger 方程式は,角度部分と動径部分に変数分離できる。
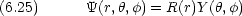
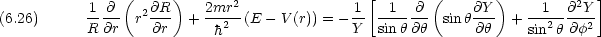
 ,
,  のみの関数なので,両辺は定数
のみの関数なので,両辺は定数  に等しいはずである。
に等しいはずである。
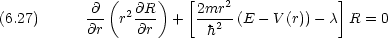
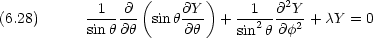
さらに
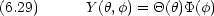
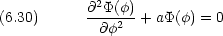

極座標を用いた応用例は,分子の回転運動,水素原子中の電子の運動を考察する場合に述べる。
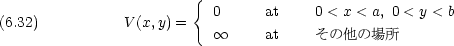
 dinger 方程式を書け。
dinger 方程式を書け。
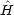 (q1,q2) =
(q1,q2) = 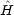 1(q1) +
1(q1) + 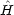 2(q2) の形に書き表すことができ
2(q2) の形に書き表すことができ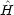 1
1 1(q1) = E1
1(q1) = E1 1(q1),
1(q1), 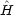 2
2 2(q2) = E2
2(q2) = E2 2(q2) であるとする。
2(q2) であるとする。
 (q1,q2) =
(q1,q2) =  1(q1)
1(q1) 2(q2) であることを示せ。
2(q2) であることを示せ。
 電子 6 個)の最長吸収波長は 255 nm である。
電子 6 個)の最長吸収波長は 255 nm である。
 電子を近似した場合,辺の長さを見積もれ。
電子を近似した場合,辺の長さを見積もれ。
 電子系に適用し,
電子系に適用し,
 電子環の半径を見積もれ。
電子環の半径を見積もれ。
 電子が10 個ある。
電子が10 個ある。
 電子を近似した場合,
電子を近似した場合,