対象とするのは,一重結合と二重結合とが交互に連なった共役
 電子系である。
電子系である。このような系では,二重目の結合を作っている
 電子はひとつの結合の部分に局在化しているのではなく,分子全体に広がっていると考えられる。
電子はひとつの結合の部分に局在化しているのではなく,分子全体に広がっていると考えられる。つまり,電子は分子の大きさ程度の箱の中を自由に飛び回っていると見なすことができる。
そのような電子のエネルギー状態は,光の吸収を測定することによって実験的にも知ることができる。
このモデルは,金属結晶中の電子にも応用できる。
一次元の箱の中の粒子の問題の具体的な応用例として,自由電子モデルを取り上げる。
対象とするのは,一重結合と二重結合とが交互に連なった共役  電子系である。
電子系である。
このような系では,二重目の結合を作っている  電子はひとつの結合の部分に局在化しているのではなく,分子全体に広がっていると考えられる。
電子はひとつの結合の部分に局在化しているのではなく,分子全体に広がっていると考えられる。
つまり,電子は分子の大きさ程度の箱の中を自由に飛び回っていると見なすことができる。
そのような電子のエネルギー状態は,光の吸収を測定することによって実験的にも知ることができる。
このモデルは,金属結晶中の電子にも応用できる。
分子中の電子は,分子全体に広がった分子軌道 molecular orbital に入っていると考えられる。
様々なエネルギー準位を持った分子軌道があるが,基底状態(最もエネルギーの低い状態)では,
低いエネルギー準位の軌道から順に 2 つづつ の電子が入っている。
電子が入っているもののうちで最もエネルギー準位の高い軌道を HOMO という
電子が入っていないもののうち最もエネルギー準位の低い軌道を LUMO という
紫外・可視光を分子が吸収すると,軌道間の電子遷移が起きる
HOMO highest occupied molecular orbital
![]() 最長波長吸収
最長波長吸収
LUMO lowest unoccupied molecular orbital
ポリエンの  電子に対するモデル
電子に対するモデル
|
共役系の長さを a とすると
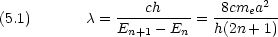
| 共役系 | N ~ N |
| 結合数 | 2n + 2 |
| 電子数 | 2n + 4 |
| 仮 定 | a = (2n + 2)r + a0, r = 0.1235 nm, a0 = 0.315 nm |
| n |  (obs)/nm (obs)/nm |
 (cal)/nm (cal)/nm |
| 1 | 309 | 309.4 |
| 2 | 409 | 409.7 |
| 3 | 511 | 510.2 |
半径 R の円軌道を質量 m の粒子が回転
円周上に原点 原点からの道のり x, 角度変数
原点からの道のり x, 角度変数 
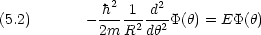
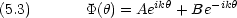
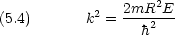
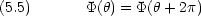
|
これを満たすためには
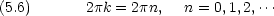
 ひとつの n に対して波動関数が無限個あるのだろうか ??
ひとつの n に対して波動関数が無限個あるのだろうか ??  と e-ik
と e-ik の一次結合で表される
の一次結合で表される 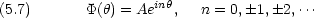
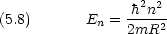
 右回りと左回り
右回りと左回り  静止
静止 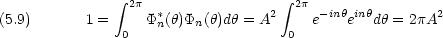
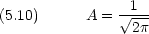
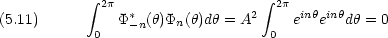
同じエネルギーで二つ以上の独立な状態がある場合,その準位は縮退(または縮重) degenerate しているという。
n 個 の状態があれば n 重縮退といい,また縮態度が n であるという。
縮退している準位の波動関数は n 個の関数のうちどれかでなければならないというものではない。 n 個の一次独立な関数の線形結合であればよい。
では, n 個の関数の選び方は一種類だけではないのではないか??  一種類だけではありません
一種類だけではありません
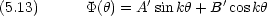
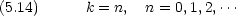
 と cosn
と cosn という選び方も可能ということである
という選び方も可能ということである  の方は n = 0 の状態はない(粒子が存在しないことになってしまう)
の方は n = 0 の状態はない(粒子が存在しないことになってしまう)
 電子 6 個)の最長吸収波長は 268 nm である。
電子 6 個)の最長吸収波長は 268 nm である。
 系の長さを見積もれ。
系の長さを見積もれ。
 に相当する光量子の波数
に相当する光量子の波数 = 1/
= 1/ (ただし
(ただし  は波長)を計算する。
は波長)を計算する。
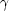 個の自由電子を持つとする。
個の自由電子を持つとする。 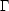 個の原子からなる一次元結晶にはどのようなエネルギー準位があり,基底状態でどのように占有されているか。
個の原子からなる一次元結晶にはどのようなエネルギー準位があり,基底状態でどのように占有されているか。