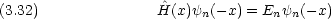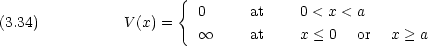dinger 方程式を具体的な問題に適用する。最初に取り扱うのは一次元の箱の中の粒子である。
dinger 方程式を具体的な問題に適用する。最初に取り扱うのは一次元の箱の中の粒子である。箱といっても一次元なので実際にはチューブの中の運動のようなものである。
数学が簡単なのでこの問題を最初に解説するのだが,物理化学的に無意味なモデルでは決してない。
たとえば分子中の電子の運動のモデルであり,三次元に拡張すれば理想気体のモデルになる。
これらの応用は次節以降で述べるが,ここでは Schr
 dinger 方程式の解法と解の性質について理解を深める。
dinger 方程式の解法と解の性質について理解を深める。
以下の章で Schr dinger 方程式を具体的な問題に適用する。最初に取り扱うのは一次元の箱の中の粒子である。
dinger 方程式を具体的な問題に適用する。最初に取り扱うのは一次元の箱の中の粒子である。
箱といっても一次元なので実際にはチューブの中の運動のようなものである。
数学が簡単なのでこの問題を最初に解説するのだが,物理化学的に無意味なモデルでは決してない。
たとえば分子中の電子の運動のモデルであり,三次元に拡張すれば理想気体のモデルになる。
これらの応用は次節以降で述べるが,ここでは Schr dinger 方程式の解法と解の性質について理解を深める。
dinger 方程式の解法と解の性質について理解を深める。
質量 m の粒子が次のポテンシャルの中を運動する
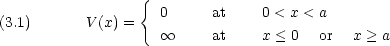
力は F = -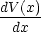 なので, 0 < x < a の範囲では F = 0 で,粒子は等速運動する。
なので, 0 < x < a の範囲では F = 0 で,粒子は等速運動する。
|x| = a の位置で粒子の受ける力 は無限大となるが,ここでは粒子と壁とが完全弾性衝突するとみなす。(エネルギーが保存するような系)。
粒子のエネ ルギーを E として
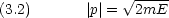
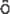 dinger 方程式
dinger 方程式
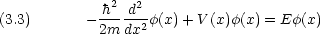
x < 0 及び x > a では V (x) =  なので方程式を満たす解は
なので方程式を満たす解は  (x) = 0 である。 0 < x < a の範囲では V (x) = 0 な
ので
(x) = 0 である。 0 < x < a の範囲では V (x) = 0 な
ので
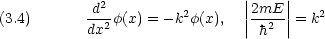
V (x) =  と V (x) = 0 の領域の境界で次の条件が課せられる。
と V (x) = 0 の領域の境界で次の条件が課せられる。
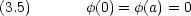
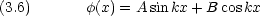
 (0) = 0 から
(0) = 0 から

 (a) = 0 から
(a) = 0 から
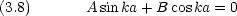
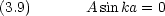
A は,境界条件のみからでは決まらない。ただし,波動関数が量子的な粒子の状態を表現しているとすれば, A = 0 は物理的に意味がない。
なぜなら,その場合  (x) = 0,つまり至る所で波動がないことになる。
(x) = 0,つまり至る所で波動がないことになる。
これは,粒子がどこにも存在しないことを意味している。物理的に意味がある解は, A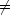 0 でかつ B = 0 であり,次の条件を満たす場合である。
0 でかつ B = 0 であり,次の条件を満たす場合である。

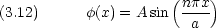
エネルギーは次のように与えられる。
一次独立な波動関数が独立な状態(準位)を表現すると考える。波動関数が一次従属であるような状態は独立ではない。 sin(-x) = -sin(x) だから, n < 0 の波動関数は単に n > 0 の波動関数に-1 を掛けたものである。よって,波動関数 が一次従属であり, n < 0 の状態と n > 0 の状態とは独立ではない。この場合は,全く同じ状態である。普通, A が になるように波動関数を書く。
一般に,同じ Hamiltonian から導かれた一次独立な波動関数は直交している。(この直交は,なす角が 90o であるという意味ではない。)
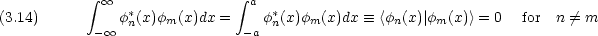
< n(x)|はブラ,|
n(x)|はブラ,| m(x)>はケットという。あわせてブラケットで,カッコの意味である。ブラとケットを組み合わせるのは, x の全範囲で積分することを表す。
m(x)>はケットという。あわせてブラケットで,カッコの意味である。ブラとケットを組み合わせるのは, x の全範囲で積分することを表す。
多次元の波動関数の場合は全空間で積分の意味になる。(ホントはベクト ルの内積として意味づけられる)
n = m の場合には,次の規格化条件が課せられる。この意味については,次節で述べる。

この条件から Aの値が決まる。 Aを規格化定数という。
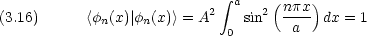
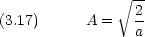
一般に,同じ Hamiltonian から導かれた一次独立な波動関数の組  n は完全系をなす。つまり,任意の関数
n は完全系をなす。つまり,任意の関数  (x) が
(x) が n(x) で次のようにかける。
n(x) で次のようにかける。
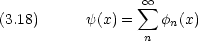
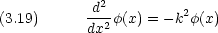
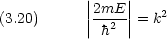
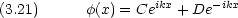
 (0) = 0 から
(0) = 0 から
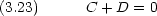
 (a) = 0 から
(a) = 0 から
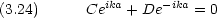
第一の条件から D = -C である。従って波動関数は
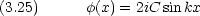
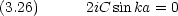
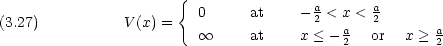
 dinger 方程式を書け。
dinger 方程式を書け。
 (a/2) =
(a/2) =  (-a/2) = 0 で与えられるとする。
(-a/2) = 0 で与えられるとする。
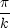 < x <
< x <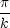 の範囲で考える。
の範囲で考える。 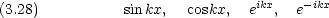
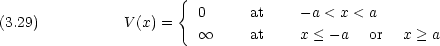


 dinger 方程式が次のように書けることを示せ。
dinger 方程式が次のように書けることを示せ。