 dinger 方程式)を知る必要がある。波動方程式は,古典的な Newton の運動方程式と対比すべき方程式であり,今後の全ての理論の出発点となる方程式である。ここでは,まず古典的な波動現象に対する方程式を解説した後,量子力学的な Schr
dinger 方程式)を知る必要がある。波動方程式は,古典的な Newton の運動方程式と対比すべき方程式であり,今後の全ての理論の出発点となる方程式である。ここでは,まず古典的な波動現象に対する方程式を解説した後,量子力学的な Schr dinger の波動方程式を示す。
dinger の波動方程式を示す。
粒子と波動の二重性を無視することのできないような量子的現象に対する理解を深めるためには,量子力学的な波動関数をつかさどる波動方程式(Schr dinger 方程式)を知る必要がある。波動方程式は,古典的な Newton の運動方程式と対比すべき方程式であり,今後の全ての理論の出発点となる方程式である。ここでは,まず古典的な波動現象に対する方程式を解説した後,量子力学的な Schr
dinger 方程式)を知る必要がある。波動方程式は,古典的な Newton の運動方程式と対比すべき方程式であり,今後の全ての理論の出発点となる方程式である。ここでは,まず古典的な波動現象に対する方程式を解説した後,量子力学的な Schr dinger の波動方程式を示す。
dinger の波動方程式を示す。
単位長さあたりの質量(密度)が 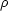 で張力 T が働いている弦の振動を考える。
で張力 T が働いている弦の振動を考える。
|
弦が平衡状態でのびた方向を x,それに対して垂直な変位の方向を y とする。弦の中で, x から x + dx 間での微小な 長さ dx の部分のみに着目し,この部分に対して Newton の方程式を考える。 F は力, m は質量, a は加速度である。

弦の微小部分 dx の y 軸方向の運動を考えた場合,慣性力 ma は
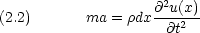
力 F は張力で決まる。張力は弦の接線方向に働く。よって,弦の平衡状態と現在の状態のなす角( at x = x,
at x = x,  at x = x + dx)によって張力の y 成分 Ty が決まる。
at x = x + dx)によって張力の y 成分 Ty が決まる。
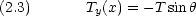
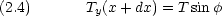
張力は弦の右端と左端とで反対方向に働くので,二式の符号は反対になる。よって力 F は
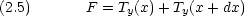
 ,
,  も小さい。その場合には sin
も小さい。その場合には sin および cos
および cos は
は  = 0 の周りに Taylor 展開できる。(
= 0 の周りに Taylor 展開できる。( も同様)
も同様)
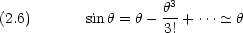
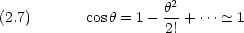
 が小さい場合には
が小さい場合には
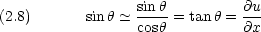
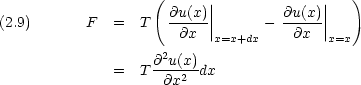
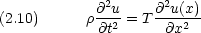
ところで,波は一定の速度 v で進むと仮定する。
時刻 t = 0 で u(x) だった波動は,変形せずに進むので,時刻 t = t には u(x - vt) になる。
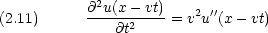
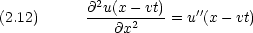
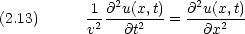
この式から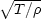 が波動の速度を表すことが解る。この式を古典的な一次元の波動方程式といい, u(x,t) を古典的波動関数という。
が波動の速度を表すことが解る。この式を古典的な一次元の波動方程式といい, u(x,t) を古典的波動関数という。
波動に周期性がある場合を考える。波長  ,波数 k,周期 T,角周波数
,波数 k,周期 T,角周波数  ,振動数
,振動数  であるとすれば,
であるとすれば,
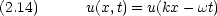

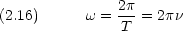
古典的波動方程式は次のようにかける
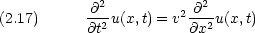

仮に
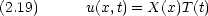
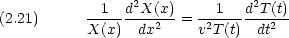
 に等しくなければならない
に等しくなければならない
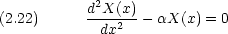
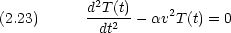
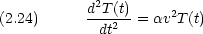
 = 0 の時には T(t) = 0 となるので意味がない。
= 0 の時には T(t) = 0 となるので意味がない。
 > 0 ならば
> 0 ならば  v2 =
v2 = 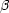 2 と置いて
2 と置いて
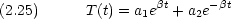
これは,振動的な波動ではなく,単調な増加または減衰を表す。 t = - または t =
または t =  で発散し,通常の波動を表すには適当でない。
で発散し,通常の波動を表すには適当でない。
 < 0 ならば av2 = -
< 0 ならば av2 = - 2 と置いて
2 と置いて
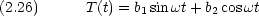
となり,角周波数  の周期的な波動を表す。定常波に対してはこのようになっていなければならない。
の周期的な波動を表す。定常波に対してはこのようになっていなければならない。
すると,古典的な波動関数は次のようにも書けることになる。
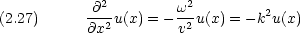
時間的に変化しない波動を定常波という。ここでは両端が固定されいる振動(たとえば弦楽器の絃)を考える。
境界条件は両端 x = 0 と x = L で振動なし,つまり u(0,t) = u(L,t) = 0 である。
変数分離型で 書くと X(0)T(t) = X(L)T(t) = 0 だから, X(x) のみに関して X(0) = X(L) = 0 である。
ところで,
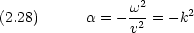
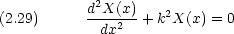
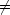 0 でなければならない。なぜなら, c1 = 0 は振動のない状態のみを表すからである。従って,境界条件を満たすためには
0 でなければならない。なぜなら, c1 = 0 は振動のない状態のみを表すからである。従って,境界条件を満たすためには
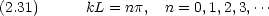
次の形の古典的波動方程式を考える。
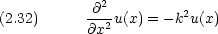
この式から, de Bloglie の物質波が従うべき方程式を導く。
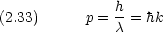
古典的に粒子のエネルギーを表すと,運動エネルギーとポテンシャルエネルギー V (x) の和なので
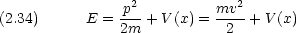
これを先の波動方程式に代入し,波動関数を u(x) の代わりに  (x) と書くと
(x) と書くと
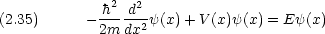
この式を時間に依存しない Schr dinger 方程式という。この式が物理化学 III と IV の内容の基礎になる方程式である。
dinger 方程式という。この式が物理化学 III と IV の内容の基礎になる方程式である。
 t であるとき振動数を求めよ。また, x(t) = Acos
t であるとき振動数を求めよ。また, x(t) = Acos t+B sin
t+B sin t であるとき,振動数を求めよ。
t であるとき,振動数を求めよ。
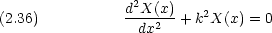
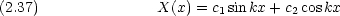
 と k との間にはどのような関係があるか。 k は波数と呼ばれる。
と k との間にはどのような関係があるか。 k は波数と呼ばれる。
 との間にはどのような関係があるか。
との間にはどのような関係があるか。
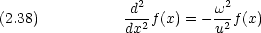

 を計算せよ。
を計算せよ。
 = 2
= 2
 は角周波数と呼ばれる。どのような意味を持つ量か。
は角周波数と呼ばれる。どのような意味を持つ量か。
 dinger 方程式を導け。
dinger 方程式を導け。
 dinger 方程式は次のように書けることが知られている。
dinger 方程式は次のように書けることが知られている。 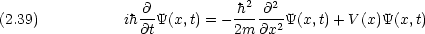
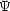 (x,t) =
(x,t) =  (x)f(t) とかけると仮定してこの方程式を変数分離し,
(x)f(t) とかけると仮定してこの方程式を変数分離し,  (x) と f(t) に対する方程式を求めよ。
(x) と f(t) に対する方程式を求めよ。 (x) に対する方程式は時間に依存しない Schr
(x) に対する方程式は時間に依存しない Schr dinger 方程式になる。
dinger 方程式になる。