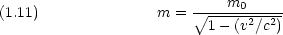1: 粒子と波動
前世紀終わりから今世紀初めにかけて,光や電子の振る舞いが明らかになるとともに,それまで知られていた古典物理学に対する問題点が認識されはじめた。この節では,光と電子が関わる興味深い現象である光電効果を例にして,光と電子にみられる粒子と波動の二重性について述べる。さらに,電子の電荷と質量を測定した有名な実験を紹介する。
1.1 光の回折と干渉〜光の波動性〜
光の本性は何かという問題に関しては古くから議論があった
Huygens (波動説)対 Newton (粒子説)
干渉・回折がみられることから波動説に落ち着いていた
1.2 光電効果 〜光の粒子性〜
金属板に X 線や紫外線(光,波長  ,強度 I )をあてると電子が飛び出す。それを,極板をおいて光電子を電流として観測する。さらに,電子が飛び出すのを阻害する方向に抑圧電圧 V をかける。
,強度 I )をあてると電子が飛び出す。それを,極板をおいて光電子を電流として観測する。さらに,電子が飛び出すのを阻害する方向に抑圧電圧 V をかける。
 >
>  t の時 I に関わらず光電子なし
t の時 I に関わらず光電子なし  <
<  t の時 I に関わらず光電子あり
t の時 I に関わらず光電子あり - 光をあてるとただちに光電子が出る
- 光電流は I に比例
I を強くすると光電子数が増える
光電子の速度が速くなるのではない
- 光電効果の生じる最大抑圧電圧 V max は
I によらない
- V max は
 が短いほど大きい
が短いほど大きい
これらの現象は光の波動説では説明できないが,もしも光が h というエネルギーを持つ粒子だったら光電効果に説明が付く。 h は Planck 定数,
というエネルギーを持つ粒子だったら光電効果に説明が付く。 h は Planck 定数,  は光の振動数である。金属原子が電子を放出するためには最低 W のエネルギーが必要であるとする。 W は仕事関数という。金属原子は一回に一粒づつの光の粒子吸収するとする。h
は光の振動数である。金属原子が電子を放出するためには最低 W のエネルギーが必要であるとする。 W は仕事関数という。金属原子は一回に一粒づつの光の粒子吸収するとする。h < W ならば,電子は放出されない。 h
< W ならば,電子は放出されない。 h > W ならば, h
> W ならば, h - W のエネルギーを持った電子が放出される。
- W のエネルギーを持った電子が放出される。
1.3 光量子・光子
光電効果の他にも光の波動説で説明できない現象がある
黒体輻射,コンプトン効果,低温の固体比熱,原子スペクトル等
では光は 100 % 粒子なのか No
No
では光は 100 % 波動なのか No
No
また, p を運動量, c を光速として
1.4 電子の電荷と質量 〜電子の粒子性〜
1.4.1 Millikan の油滴実験
電子の電荷を測定する実験
油滴を帯電させる
電荷は電子の電荷の整数倍 Ze のはずである
まず,油滴の落下速度を測る
重力,空気による浮力,空気からの摩擦力がつりあう
摩擦力 F = 6
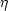 Rv
Rv
落下速度 v から油滴の半径 R と質量 m とがわかる
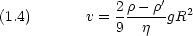
F : 空気による抵抗力, h : 空気の粘度,
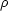
: 油滴の密度,
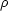
' : 空気の密度, g : 重力加速度
次に落下している油滴に上下から電場 E をかけて静止させる
重力と電場による力とがつりあう
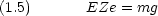
多くの油滴について測定を繰り返せば e がわかる
電気素量 e = 1.6217733 × 10
-19 C
1.4.2 Thomson の陰極線の実験
電子の電荷割る質量 e/me を測定する実験
陰極線を発生させる
A で電場をかけ陰極線を屈曲させる
スクリーン上で O からの変位を測定
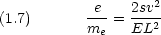
v : 陰極線中の電子の速度, m
e : 電子の質量
電場の効果を打ち消すように磁場 H をかけると v がわかる

これから e/m
e がわかる
電子の静止質量 me = 9.1093897×10-31kg
「静止」質量 高速の粒子では相対論的な効果を考える必要がある
高速の粒子では相対論的な効果を考える必要がある
1.5 電子線回折 〜電子の波動性〜
電子をビーム状に飛ばした電子線が光と同様の回折現象を示すことが,Davisson と Germer によって 1927年 に示された。これは,それまで粒子だと考えられていた電子が波動としての性質を持つことを示している。
1.6 物質波 de Broglie wave
電子だけでなく,いままで粒子であると思っていた物質は一般に波動としての性質を持っている。そのような波動を物質波という。
物質波の波長が十分短ければ,粒子と見なして差し支えない。
物質波の考え方は,光量子の裏返しとして, 1923年に de Broglie によって提唱された。これは,電子線回折現象の発見以前のことである。
演習問題
- 100 W の水銀灯がある。
- 100 W は 1 s に何 J のエネルギーを消費していることに相当するか。
- 光源から 1 m 離れた場所で,単位時間単位面積あたりのエネルギーの流れはどれだけか。水銀灯の 効率は 100 % であるとする。
- そこに置かれた金属原子が 1 s に受け取るエネルギーはどれだけになるか。金属原子の直径は 1 Åで,エネルギー吸収効率は 100 %
であるとする。
- 光は完全に波動であるとして,金属の仕事関数が 2 eV である時,光電子が飛び出すのに必要なエ ネルギーを吸収するまでにどれくらいの時間がかかるか。
- 光電効果に関する実験事実が光の波動説と矛盾する点についてのべよ。
- Na の光電効果について。
- Na の仕事関数 W は 1.82 eV である。光電効果が生じる最長波長
 t
を計算せよ。
t
を計算せよ。
- Na に波長 250 nm の光を照射した。光電効果が生じる最大の抑制電圧 V max を計算せよ。
- Li の光電効果について。照射光 300 nm の時 V max = 1.83 V, 400 nm の時 V max = 0.80 V であ る。
- 仕事関数 W を見積もれ。
- Planck 定数 h を見積もれ。
- 光電効果の生じる最長波長
 t
を計算せよ。
t
を計算せよ。
- K 金属は,波長 552 nm 以上の光では光電効果を示さない。
- 仕事関数 W を見積もれ。
- 照射光 300 nm,抑制電圧ゼロの時,光電子の運動エネルギーを見積もれ。
- 照射光 400 nm の時,光電効果が生じる最大の抑制電圧 V max を計算せよ。
- Cr 金属は, 4.40 eV の仕事関数を持つ。
- 光電効果が生じる最長波長
 t を計算せよ。
t を計算せよ。
- 波長 200 nm の光を照射した。光電効果が生じる最大の抑制電圧 V max を計算せよ。
- Ag の光電効果について。照射光 230 nm の時 V max = 0.80 V である。
- 仕事関数 W を見積もれ。
- 最長波長
 t を計算せよ。
t を計算せよ。
- 次の場合に物質波の波長を計算せよ。単位を明記すること。
- 体重 60 kg の人間が 100 m を 10 s で走る時。
- 150km h-1 の野球のボール。質量 140 g 。
- 2.7 × 103 m s-1 で飛ぶ陽子。
- 運動エネルギー 7 × 10-19 J で金箔から飛び出した光電子。
- 次の運動エネルギーを持つ電子の場合に物質波の波長を計算せよ。単位を明記すること。
(1) 1 eV (2) 100 eV (3) 10 keV
- 電子が光速 c の 4 分の 1 の速さで飛んでいる。
- 相対論的な効果を無視して,物質波の波長を計算せよ。
- 相対論によると,静止質量 m0 の物体が速度 v で運動するときの質量は次のように表され る。
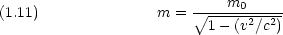
相対論的効果を考慮に入れて物質波の波長を計算せよ。
- 電子の速度が光速の 1000 分の 1 である時, (1), (2) と同様の問に答えよ。
- 電子の物質波の波長を 0.1 nm 程度にするためにはどの程度の電圧で加速する必要があるか計算せ よ。
- 出力が 10 mW である時,次のレーザーは 1 s 間にいくつの光子を放出しているか。
| (1) |
|
He-Ne レーザー |
|
波長 633 nm |
| (2) |
|
Ar+ レーザー |
|
波長 529 nm |
| (3) |
|
Ar+ レーザー |
|
波長 355 nm |
| (4) |
|
He + Cd+ レーザー |
|
波長 325 nm |
- 次の波長の光子の振動数,波数,運動量を見積もれ。
(1) X 線 1 nm (2) 紫外線 250 nm (3) 可視光 500 nm (4) 赤外線 1 mm
(5) マイクロ波 1 mm (6) ラジオ波 100 m
- 水素原子をイオン化するには最低 13.60 eV のエネルギーが必要である。水素をイオン化し得る光の最長波長を見 積もれ。
 ,強度 I )をあてると電子が飛び出す。それを,極板をおいて光電子を電流として観測する。さらに,電子が飛び出すのを阻害する方向に抑圧電圧 V をかける。
,強度 I )をあてると電子が飛び出す。それを,極板をおいて光電子を電流として観測する。さらに,電子が飛び出すのを阻害する方向に抑圧電圧 V をかける。
 ,強度 I )をあてると電子が飛び出す。それを,極板をおいて光電子を電流として観測する。さらに,電子が飛び出すのを阻害する方向に抑圧電圧 V をかける。
,強度 I )をあてると電子が飛び出す。それを,極板をおいて光電子を電流として観測する。さらに,電子が飛び出すのを阻害する方向に抑圧電圧 V をかける。
 >
>  t の時 I に関わらず光電子なし
t の時 I に関わらず光電子なし  <
<  t の時 I に関わらず光電子あり
t の時 I に関わらず光電子あり  が短いほど大きい
が短いほど大きい というエネルギーを持つ粒子だったら光電効果に説明が付く。 h は Planck 定数,
というエネルギーを持つ粒子だったら光電効果に説明が付く。 h は Planck 定数,  は光の振動数である。金属原子が電子を放出するためには最低 W のエネルギーが必要であるとする。 W は仕事関数という。金属原子は一回に一粒づつの光の粒子吸収するとする。h
は光の振動数である。金属原子が電子を放出するためには最低 W のエネルギーが必要であるとする。 W は仕事関数という。金属原子は一回に一粒づつの光の粒子吸収するとする。h < W ならば,電子は放出されない。 h
< W ならば,電子は放出されない。 h > W ならば, h
> W ならば, h - W のエネルギーを持った電子が放出される。
- W のエネルギーを持った電子が放出される。
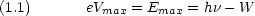
 No
No No
No
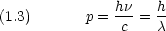

 Rv
Rv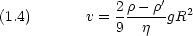
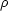 : 油滴の密度,
: 油滴の密度,  ' : 空気の密度, g : 重力加速度
' : 空気の密度, g : 重力加速度
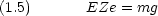
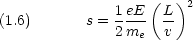
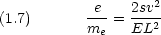


 高速の粒子では相対論的な効果を考える必要がある
高速の粒子では相対論的な効果を考える必要がある

 t
を計算せよ。
t
を計算せよ。
 t
を計算せよ。
t
を計算せよ。
 t を計算せよ。
t を計算せよ。
 t を計算せよ。
t を計算せよ。